The property rights approach to moral uncertainty

by Harry R. Lloyd | October 2022

Moral Uncertainty | Philosophy | Theoretical Research

Given the current state of our moral knowledge, it is entirely reasonable to be uncertain about a wide range of moral issues. This paper considers the suggestion that appropriateness under moral uncertainty is a matter of dividing one’s resources between the moral theories in which one has credence, allowing each theory to use its resources as it sees fit.

Download Report as PDF

This report was produced as part of the Happier Lives Institute’s 2022 Summer Research Fellowship¹

1. Introduction

Distribution: Imagine that some agent J is devoting her life to ‘earning to give’: J is pursuing a lucrative career in investment banking and plans to donate most of her lifetime earnings to charity. According to the moral theory T_health in which J has 60% credence, by far and away the best thing for her to do with her earnings is to donate them to global health charities, and the next best thing is to donate them to charities that benefit future generations by fighting climate change. On the other hand, according to the moral theory T_future in which J has 40% credence, by far and away the best thing for her to do with her earnings is to donate them to benefitting future generations, and the next best thing is to donate them to global health charities.² On all other issues, T_health and T_future are in total agreement: for instance, they agree on where J should work, what she should eat, and what kind of friend she should be. They only disagree about which charity J should donate to. Finally, neither T_health nor T_future is risk loving: each theory implies that an $x donation to a charity that the theory approves of is at least no worse than a risky lottery over donations to that charity whose expected donation is $x. In light of her moral uncertainty, what is it appropriate for J to do with her earnings?³

According to one prima facie plausible proposal, it is appropriate for J to donate 60% of her earnings to global health charities and 40% of them to benefitting future generations – call this response Proportionality. Despite Proportionality’s considerable intuitive appeal, none of the theories of appropriateness under moral uncertainty thus far proposed in the literature support this simple response to Distribution.

In this paper, I propose and defend a Property Rights Theory (henceforth: PRT) of appropriateness under moral uncertainty, which supports Proportionality in Distribution.⁴

One might worry that the Proportional response to Distribution likewise reflects an irrational bias or heuristic (I thank Martin Vaeth for suggesting this objection.) In response, I report that my personal intuitions in favour of the Proportional response to Distribution are far more robust to reflection than any intuitions that I have in favour of Proportional responses to empirical uncertainty. Moreover, I argue in §4.4 below that normative uncertainty differs in several important respects from empirical uncertainty. An irrational response to empirical uncertainty might be a perfectly rational response to normative uncertainty (and vice versa). In §2.1, I introduce the notion of appropriateness. In §2.2, I introduce several of the theories of appropriateness that have been proposed thus far in the literature. In §2.3, I show that these theories fail to support Proportionality. In §§3.1-3.3, I introduce PRT and I demonstrate that it supports Proportionality in Distribution. In §§3.4-3.9, I discuss the details. In §3.10, I extend my characterisation of PRT to cover cases where an agent faces a choice between discrete options, as opposed to resource distribution cases like Distribution.⁵ In §4, I argue that PRT compares favourably to the alternatives introduced in §2.2. In §5, I conclude.

2. Alternatives to the Property Rights Theory

2.1 Appropriateness

Suppose I believe that animal suffering does not matter morally, but also that I am somewhat uncertain about this. If animal suffering matters morally, then I am required to eat tofu rather than foie gras, whereas if animal suffering does not matter morally, then I am permitted to eat either tofu or foie gras. In view of my moral uncertainty, there is plausibly some sense in which it is inappropriate for me to eat the foie gras rather than the tofu.⁶

In this paper, I shall discuss competing normative theories about which actions are appropriate under moral uncertainty. I shall not discuss the metaethical question of how we should understand this intuitive notion of ‘appropriateness’. Instead, I shall tentatively adopt MacAskill, Bykvist and Ord’s suggestion that to call some choice ‘appropriate’ is to say that this choice would be rational for the decision maker, if she were “morally conscientious”.⁷ Morally conscientious agents “care about doing right and refraining from doing wrong” and “also care more about serious wrong-doings than minor wrong-doings.”⁸ MacAskill, Bykvist and Ord “take this to be a precisification of the ordinary notion of conscientiousness, loosely defined as ‘governed by one’s inner sense of what is right,’ or ‘conforming to the dictates of conscience.’”⁹

2.2 Theories of appropriateness

The first theory of appropriateness that I discuss in this section is My Favourite Theory (henceforth: ‘MFT’).¹⁰ To a first approximation, MFT says that:

an action A is appropriate in some choice situation χ iff according to the theory that the decision maker has most credence in, A is maximally choiceworthy in χ.¹¹

The choiceworthiness of an action in some choice situation according to some moral theory is the strength of the decision maker’s moral reasons in favour of performing that action according to that moral theory.¹² In other words, A is more choiceworthy than B according to some moral theory T iff the decision maker’s moral reasons in favour of A are stronger than her moral reasons in favour of B according to T.

MFT arguably has implausible implications in certain cases where the decision maker has strictly positive credence in (henceforth: ‘entertains’) a large number of theories.¹³ Suppose that the theories T₁, …, T₉₈ all agree that action A is the best option available to the decision maker in some choice situation and that action B is the worst. However, theory T₉₉ says that B is the best option and A is the worst. The decision maker has credence 0.01 in each of the theories T₁, …, T₉₈ and credence 0.02 in T₉₉. According to MFT, action B is the only appropriate option for that decision maker in this situation.

One way to avoid this result is to adopt My Favourite Option (henceforth: ‘MFO’). According to MFO:

an action A is appropriate in some situation χ iff for any other option B that is available to the decision maker in χ, the decision maker’s credence in A being maximally choiceworthy in χ is greater than or equal to her credence in B being maximally choiceworthy in χ.¹⁴

In the case that I use to critique MFT, the decision maker has credence 0.98 in A being maximally choiceworthy, and credence 0.02 in B being maximally choiceworthy. Hence, MFO implies that option A is uniquely appropriate.

Both MFT and MFO arguably have implausible implications in so-called ‘Jackson cases’.¹⁵

Jackson: In some situation, suppose that according to T₁: A is the best option; B is almost as good; and C is terrible. According to T₂: C is the best option; B is almost as good; and A is terrible. Furthermore, suppose that the decision maker has credence 0.51 in T₁, and 0.49 in T₂ (see Figure 1).

Figure 1: Jackson cases

According to both MFT and MFO, it is uniquely appropriate for the decision maker to choose option A in Jackson. Yet many of us intuit, to the contrary, that it is uniquely appropriate for the decision maker to ‘hedge her bets’ by choosing option B. After all, the decision maker is certain that B is near-maximally choiceworthy. By contrast, she has credence 0.49 in option A being terrible. Hence option B seems more appropriate than option A.¹⁶

T₁ and T₂ are intertheoretically unit-comparable iff for any actions A, B, C, and D, there exists some k for which it is true and meaningful to say that the difference in choiceworthiness between A and B according to T₁ is k times the size of the difference in choiceworthiness between C and D according to T₂.¹⁷. In cases where T₁ and T₂ are intertheoretically unit-comparable, one option for honouring our intuitions about Jackson is to Maximise Expected Choiceworthiness (henceforth: ‘MEC’).¹⁸ According to MEC:

an action is appropriate in some situation iff it maximises intertheoretic expected choiceworthiness.¹⁹

Secondly, what about cases where one or more of the entertained theories ranks options ordinally rather than cardinally? Perhaps the simplest proposal open to advocates of MEC here is to suggest that one should somehow cardinalize the ordinal theories. After that, one can simply Maximise Expected Normalized Choiceworthiness (MacAskill, Bykvist and Ord 2020, pp. 108-10). For criticisms of and two alternatives to this theory-by-theory cardinalization approach, see Tarsney 2021; [redacted]. Cf. also Tarsney 2019a; Carr 2022; Pivato 2022; Gustafsson forthcoming.

The intertheoretic expected choiceworthiness of some action is a weighted average of its choiceworthiness according to each of the entertained theories, where each theory’s weight is equal to the decision maker’s credence in that theory.²⁰ Suppose, for instance, that in Jackson, T₁ and T₂ are intertheoretically unit-comparable, and their choiceworthiness schedules are as follows:

Table 1a

Choiceworthiness	T₁: 0.51 credence	T₂: 0.49 credence
A	10	–10
B	9	9
C	–10	10

Hence, A’s expected choiceworthiness is (0.51 x 10) + (0.49 x -10) = 0.2, B’s expected choiceworthiness is (0.51 x 9) + (0.49 x 9) = 9, and C’s expected choiceworthiness is (0.49 x 10) + (0.51 x -10) = -0.2.

Table 1b

Choiceworthiness	T₁: 0.51 credence	T₂: 0.49 credence	Intertheoretic expectation
A	10	–10	0.2
B	9	9	9
C	–10	10	–0.2

Thus, B uniquely maximises expected choiceworthiness in this situation.

The final theory of appropriateness that I introduce in this section is Greaves and Cotton-Barratt’s Nash Bargaining Theory (henceforth: ‘NBT’).²¹ NBT is only applicable in cases where all of the entertained theories’ choiceworthiness orderings can be represented by von Neumann-Morgenstern (henceforth: ‘vNM’) choiceworthiness functions. A choiceworthiness function is vNM iff the ex-ante choiceworthiness of bringing about any lottery L over two or more possible outcomes is equal to a weighted average of the choiceworthinesses of risklessly bringing about each of L’s possible outcomes, where each possible outcome’s weight in this average is its probability of occurring under L. For instance, suppose that according to some vNM representation of T’s choiceworthiness ordering, A and B have choiceworthiness values 8 and 4 respectively. Then the ex-ante choiceworthiness of a fifty-fifty lottery over A and B must be (0.5 x 8) + (0.5 x 4) = 6.

In cases where all of the entertained theories are vNM representable, NBT says that one should model the set of entertained theories as a set of bargainers. In each choice situation, the bargainers will bargain with each other over which action is to be performed. The greater the decision maker’s credence in some entertained theory, the greater the ‘leverage’ with which its bargainer will enter the bargaining problem. A popular solution concept for such bargaining problems is the Nash Bargaining Solution; in particular, Greaves and Cotton-Barratt use the Asymmetric Nash Bargaining Solution, whose technicalities I relegate to the appendix. According to Greaves and Cotton-Barratt’s NBT:

an action is appropriate in some situation iff it is an Asymmetric Nash Bargaining Solution of the corresponding bargaining problem.

Greaves and Cotton-Barratt themselves “tentatively” reject this theory in favour of MEC.²²

My statement of NBT is somewhat ambiguous, since it does not specify how to construct the bargaining problems ‘corresponding’ to any particular choice situations. In particular, I have not specified how to select the disagreement point for these bargaining problems. The ‘disagreement point’ in any bargaining problem is the outcome that the bargainers believe will eventuate if they do not together settle on a negotiated agreement. Greaves and Cotton-Barratt suggest that in the application of bargaining theory to moral uncertainty, “it is unclear how the disagreement point should be identified. The talk of different theories ‘bargaining’ with one another is only metaphorical, and there is not obviously any empirical fact of the matter regarding ‘what would happen in the absence of agreement.’”²³ According to Greaves and Cotton-Barratt, NBT theorists should simply “select some disagreement point such that bargaining theory with that choice of disagreement point supplies a satisfactory” theory of appropriateness.²⁴

Greaves and Cotton-Barratt do not decide in favour of any particular disagreement point. Instead, “as far as possible” they “proceed in a way that is independent of how the disagreement point is identified.”²⁵

Possible disagreement points mentioned by Greaves and Cotton-Barratt include:

Random dictator: a lottery is held, wherein each bargainer’s chance of winning is equal to the decision maker’s credence in the moral theory represented by that bargainer. The lottery winner gets to decide how the decision maker will act in the current choice situation.
Anti-utopia: an outcome whose choiceworthiness according to any given moral theory is the minimum choiceworthiness possible in this choice situation according to that moral theory.
Do nothing: the outcome that would eventuate if the decision maker did nothing.

2.3 Proportionality

So much for the finer points of NBT. I now show that MFT, MFO, MEC, and NBT do not support Proportionality in Distribution. First, I consider MFT and MFO. Recall that agent J in Distribution has 60% credence in T_health and thus 60% credence in it being uniquely maximally choiceworthy to donate to global health charities in Distribution. Hence, both MFT and MFO imply that it is most appropriate, contra Proportionality, for J to donate all of her money to global health charities. This is an intuitive disadvantage of these theories.

In order to apply MEC to Distribution, let us suppose that the choiceworthiness evaluations of T_health and T_future are intertheoretically unit-comparable. For sake of concreteness, suppose that according to T_health, one dollar donated to global health charities does five times as much good as one dollar spent on benefitting future generations, and vice versa according to T_future. In particular, if h% of J’s money is spent on global health, and (100–h)% is spent on benefitting future generations, then choiceworthiness according to T_healthis 5h + (100 – h) = 100 + 4h, whereas choiceworthiness according to T_future is h + 5(100 – h) = 500 – 4h. Intertheoretically expected choiceworthiness as a function of h is therefore 0.6(100 +4h) + 0.4(500 – 4h) = 260 + 0.8h

Figure 2: Choiceworthiness as a function of h

Figure 2: Choiceworthiness as a function of h

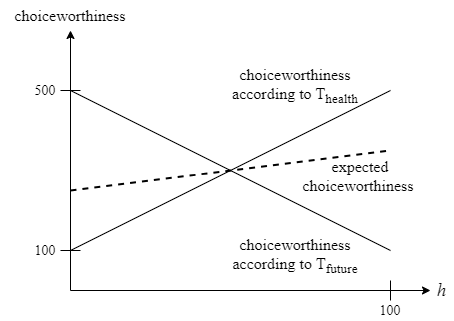
Expected choiceworthiness is clearly maximised when h is as large as possible. Hence, under these assumptions, MEC implies that it is most appropriate, contra Proportionality, for J to donate all of her money to global health charities. In general, MEC only ever implies Proportionality as a matter of coincidence.

Greaves and Cotton-Barrat’s NBT comes much closer than MFT, MFO, and MEC to supporting Proportionality. Indeed, if (as in Figure 2) T_health and T_future can both be represented by vNM choiceworthiness functions that are linear in h, then the random dictator and anti-utopia versions of NBT will both support Proportionality as an appropriate response to Distribution.²⁶ A vNM choiceworthiness function linear in h corresponds to risk neutrality with respect to h. In other words: the choiceworthiness of a lottery over two or more different values of h is always equal to the choiceworthiness of the expected value of h under that lottery.

Under the random dictator lottery in Distribution, h = 100 is chosen with 60% probability, and h = 0 is chosen with 40% probability, yielding 60 as the expected value of h. Hence, if T_health and T_future can both be represented by vNM choiceworthiness functions that are linear in h, then an outcome is no less choiceworthy than the random dictator point according to both T_health and T_future iff that outcome is no less choiceworthy than h = 60 according to both T_health and T_future. Of course, T_health prefers h to be as large as possible, whereas T_future prefers h to be as small as possible. Hence, every expected value of h other than 60 is less choiceworthy than the random dictator point according to either T_health or T_future. For this reason, if T_health and T_future can both be represented by vNM choiceworthiness functions that are linear in h, then the random dictator version of NBT supports Proportionality as an appropriate response to Distribution.²⁷

Under this linearity condition, the anti-utopia version of NBT also supports Proportionality in Distribution.²⁸ For want of space, I prescind from explaining here why this result obtains.

In summary: if T_health and T_futurecan both be represented by vNM choiceworthiness functions that are linear in h, then at least two of Greaves and Cotton-Barratt’s versions of NBT support Proportionality in Distribution.

However, in a great many cases where one or both of the vNM choiceworthiness functions for T_health or T_future are non-linear in h, both the random dictator and the anti-utopia versions of NBT imply that Proportionality is inappropriate in Distribution. For instance, suppose that T_health is risk averse with respect to h, so that the choiceworthiness ordering of T_health can be represented by the concave vNM choiceworthiness function √(h/100). In other words: according to T_health, the choiceworthiness of a lottery over two or more different values of h is always lower than the choiceworthiness of the expected value of h under that lottery. By contrast, suppose that T_future is risk neutral, so that its choiceworthiness ordering can be represented by the vNM choiceworthiness function 1 – (h/100) (see Figure 3).

Figure 3: Choiceworthiness as a function of h

Recall that in Distribution, under the random dictator lottery h = 100 is chosen with 60% probability, and h = 0 is chosen with 40% probability, yielding 60 as the expected value of h. Since T_future is risk neutral with respect to h, an outcome is no less choiceworthy than the random dictator point according to T_future iff in expectation, h ≤ 60. By contrast, because T_health is somewhat risk averse with respect to h, certain low-risk outcomes are no less choiceworthy than the random dictator point according to T_health even though these outcomes yield expected values of h strictly less than 60. For instance, according to T_health, h = 36 with certainty is no less choiceworthy than the random dictator point, since √(36/100) = 0.6 = (0.6 x 1) + (0.4 x 0).

Thus, under a random dictator disagreement point, bargainers are disadvantaged to the extent that they are risk averse.²⁹ A risk-averse bargainer is willing to accept a less-than Proportional share of the available resources in order to avoid the risk of getting nothing if no agreement is reached. In the particular example under discussion, the random dictator version of NBT implies, contra Proportionality, that it is appropriate for J to spend only half of her money on global health charities. The anti-utopia version of NBT also has this implication.³⁰ I can see no reason why appropriateness in Distribution should depend in this way on each theory’s degree of risk aversion. Bear in mind here that vNM choiceworthiness functions need not be ‘interval-scale’ measures of choiceworthiness.³¹

Another important disadvantage of NBT is that in cases where the choiceworthiness rankings of either T_health or T_future are non-vNM, NBT is simply inapplicable.³²

Explaining a little further: the (Asymmetric) Nash Bargaining Solution is only invariant up to affine transformations of the bargainers’ utility functions. Hence, for NBT to be applicable, (1) the class of affine transformations of the chosen functional representations of the entertained theories’ choiceworthiness orderings must be somehow privileged over any other possible representations of those orderings. Furthermore, (2) the feasible set must be convex in order for the (Asymmetric) Nash Bargaining Solution to satisfy its characteristic axioms. In many cases where one or more of the bargainers have non-vNM preferences, conditions (1) and/or (2) are violated. Restricting the applicability of the (Asymmetric) Nash Bargaining Solution to cases where all of the bargainers have vNM preferences is the generally accepted way to ensure that conditions (1) and (2) are both satisfied. For instance, suppose that T_health or T_future is a risk avoidant moral theory, according to which the ex-ante choiceworthiness of bringing about some risky lottery L over two or more possible outcomes is more sensitive to the choiceworthiness of risklessly bringing about L’s worst possible outcome than it is in a vNM-representable moral theory.³³ (The difference between vNM-representable and risk-avoidant moral theories is illustrated in Figure 4) NBT is ex hypothesi inapplicable to a decision maker who has any positive credence in any risk-avoidant moral theories. This is a significant disadvantage of NBT.

Figure 4: vNM-representable and risk-avoidant moral theories

Sergio Tenenbaum has also recently argued that the best version of deontology need not be vNM. According to Tenenbaum, “deontological rules, prohibitions, and permissions apply primarily to intentional acts; [and] risk changes the nature of an [intentional] act, not the probability that the same act will be performed,” thus undercutting an important motivation for vNM representability.³⁴ Once again, NBT is inapplicable to a decision maker – like Sergio Tenenbaum – who has positive credence in any non-vNM versions of deontology. This is a significant disadvantage of NBT.

3. The Property Rights Theory

3.1 The basic idea

The idea behind NBT is that the decision maker’s entertained moral theories should be modelled as bargainers, who in each choice situation bargain with each other over which action will be performed. Relatedly, the idea behind certain voting-inspired theories of appropriateness – such as MacAskill’s Borda Count Theory³⁵ – is that the decision maker’s entertained moral theories should be modelled as voters, who in each choice situation hold a vote to determine which action will be performed.³⁶

The idea behind PRT is that what is appropriate in each choice situation χ is determined by a certain economic model of χ. Each entertained moral theory T_i is modelled as a property-owning economic agent A_i, who has open to her all of the options open to the decision maker. In a resource distribution choice situation like Distribution, each theory-agent A_iis initially endowed with a share of the decision maker’s resources proportional to the decision maker’s credence in the corresponding theory T_i. A_i initially owns these resources, and can use them as she sees fit (this is how the ‘Property Rights’ Theory gets its name). For instance, A_i can spend her resources in any of the ways open to the decision maker. Theory-agents can also make contracts with each other governing how they will use their resources. A_i’s preference structure over the space of possible outcomes of the model is identical to T_i’s choiceworthiness structure over the corresponding space of actions open to the decision maker.³⁷ Finally, A_i is certain that T_i is true. An option is appropriate in χ iff it is the aggregate of all of the actions performed by the decision maker’s theory-agents in an equilibrium of the economic model of χ.³⁸

PRT can be understood as a particular kind of bargaining theory, since economic agents interacting with each other in an exchange economy are eo ipso bargainers. In this respect, NBT and PRT have something in common. On the other hand, there are several fundamental differences between NBT and PRT. Footnote 39 provides a résumé of those differences.³⁹

(1) As I explain in §3.2, the motivating ideas are different. Or at least: PRT’s motivating idea is more specific than NBT’s. Free markets always involve some element of bargaining, but not all bargaining problems take place in free markets. For instance, peace treaty negotiations can be modelled as bargaining problems, even though they are clearly not examples of market interactions. Unlike NBT, PRT is specifically inspired by the market system.

(2) As I explain in §3.5, PRT uses Position Maximin rather than the Asymmetric Nash Bargaining Solution to solve the bargaining problem between theory-agents. For this reason, PRT but not NBT is applicable in cases where one or more of the entertained theories is non-vNM.

(3) As I explain in §3.7, PRT has ‘broader scope’ than NBT, and hence avoids the problem of scenario individuation (cf. n. 22 above).

(4) Relatedly, the revisions to PRT introduced in §3.9 have no parallels in Greaves and Cotton-Barratt’s NBT.

(5) The ‘disagreement point’ used in PRT’s model of resource-distribution choice situations is different from any of the disagreement points proposed by Greaves and Cotton-Barratt (2019, §3.1).

(6) Relatedly, my approach to choosing a disagreement point is very different from Greaves and Cotton-Barratt’s. According to Greaves and Cotton-Barratt (2019, §3.1), one should simply “select some disagreement point such that NBT with that choice of disagreement point supplies a satisfactory” theory of appropriateness. By contrast, PRT’s disagreement point follows from the motivating idea of PRT. In resource distribution cases like Distribution, each theory-agent is endowed with her fair share of the decision maker’s resources. And as I explain in §3.10, in choices between two or more discrete options, each theory-agent is endowed with her fair chance to win the lottery to decide which action is to be performed.

(7) Implicit in Greaves and Cotton-Barratt’s presentation of NBT is the assumption that each theory-agent’s beliefs about what would happen if the decision maker were to perform any action are identical to the decision maker’s own beliefs about this. PRT largely shares this assumption; but it also departs from it in one crucial respect, as I explain in §4.2. This departure allows PRT to provide an account of the value of moral information (which Greaves and Cotton-Barratt do not discuss).

3.2 Motivation

The motivating idea behind PRT is that the problem of decision making under moral uncertainty is closely analogous to the problem of incompossible preferences fundamental to microeconomics. One part of this problem is the problem of scarcity, which has been faced by every society in history. The problem of scarcity arises because there are too few resources available for every individual to be able to satisfy all of their desires for resources. Hence, any society has to decide how its finite resources will be allocated, with every allocation profile having an opportunity cost. A system of property rights and free markets is an elegant way of resolving this problem of scarcity. The initial distribution of property rights determines who is initially entitled to each unit of resources. Property owners can then trade resources with each other on the free market. Under idealised conditions of perfect information and perfect rationality, these trades will always be Pareto improvements: each agent will value what she is buying more than she values what she is selling. This is a desirable feature of the market response to the problem of scarcity.

The problem of scarcity is not the only element of the problem of incompossible preferences. Another element concerns incompossible preferences about individual behaviour. Suppose, for instance, that I know some embarrassing things about your personal life. I want to gossip to others about them, and so does the National Enquirer; but you would prefer for me to keep quiet. Logically necessarily, only one of these two preferences can be satisfied. Once again, a market system can determine which one it will be. Supposing that the law does not classify my gossip as defamatory, I am initially endowed with the right to share this gossip with whomsoever I choose. However, I also have the option to sell you that right, in the form of a nondisclosure agreement (you would pay me to sign a contract promising not to share my gossip with anyone). Under conditions of perfect information and perfect rationality, these kinds of trades are always Pareto improvements. I will sign the nondisclosure agreement only if I value the money you will pay me more than I value the right to share my gossip with the National Enquirer. Once again, this is a desirable feature of the market response to incompossible preferences.

Speaking metaphorically, being morally uncertain is a bit like being pulled in several different directions by several different parts of oneself. For instance, perhaps the dominant part of me is utilitarian, and so pulls me in the direction of maximising total utility. But perhaps another part of me is Kantian, and so pulls me in the direction of acting only according to the maxims that I can will to become universal laws. Each part of oneself has its own preferences over how one should act. In my experience, this way of describing things rings true to the particular phenomenology of moral uncertainty. The challenge for a theory of appropriateness is to derive a coherent decision rule from this collection of competing preferences.

Decision making under moral uncertainty is closely analogous to the economic problem of incompossible preferences. First, the problem of moral uncertainty is in part a problem of resource scarcity.⁴⁰ If J had unlimited resources in a case like Distribution, then she could afford to donate unlimited amounts of money to both Health and T_future’s favourite charities – enough for both charities to have more than enough money than they would know what to do with. Without resource scarcity, moral uncertainty in Distribution is unproblematic. Alternatively, suppose that some transplant surgeon has some credence in both utilitarianism and deontology. This surgeon has the option to murder one of her patients in order to harvest and transplant the patient’s organs, thereby saving five other people. If there is a shortage of organs for transplant, then the surgeon faces the problem of decision making under moral uncertainty. However, if the surgeon already has unlimited access to organs for transplant, then utilitarianism and deontology agree that she should not murder the patient. Once again, without resource scarcity moral uncertainty is unproblematic.

However, resource scarcity is not the only element of the problem of decision making under moral uncertainty. Another element concerns incompossible evaluations of individual behaviour. In Jackson, for instance, T₁ claims that the agent should perform option A, whereas T₂ claims that the agent should perform option C. Moreover, it might well be logically necessary that at most one of these two preferences can be satisfied. In that case, no amount of extra resources in Jackson could dissolve the problem of decision making under moral uncertainty. This case would then be analogous to interpersonal cases of incompossible preferences about individual behaviour such as the gossip case discussed above.⁴¹

To summarise: the problem of decision making under moral uncertainty is closely analogous to the economic problem of incompossible preferences. One elegant solution to the economic problem is a system of property rights and free markets. Under idealised conditions, this system has certain attractive properties: the initial distribution of property rights can be arranged such that each agent receives her fair share; and then free trade ensures Pareto optimality. This motivates the suggestion that an analogous Property Rights approach to the problem of moral uncertainty is worthy of investigation.

3.3 Distribution

For a simple illustration of PRT, consider Distribution. PRT says that we should model T_health and T_future as property-owning economic agents – A_health and A_future respectively – whose preference structures over outcomes are simply the choiceworthiness structures of T_health and T_future over the corresponding actions. A_health is initially assigned ownership of 60% of the decision maker’s philanthropic budget, and A_future is initially assigned ownership of the remaining 40%. If A_health and A_future wish, they can trade and make contracts with each other. They can also choose to spend their endowments in any of the ways open to J. In Distribution, as it happens, A_health and A_future do not have anything to gain by trading or making contracts with each other. A_health just wants to donate all of her endowment to global health charities, and A_future just wants to donate all of her endowment to climate change charities. Hence, according to PRT, it is appropriate for J to donate 60% of her earnings to global health charities, and 40% of her earnings to climate change charities. Proportionality is vindicated in Distribution.

3.4: Double Distribution

Distribution is a simple scenario in which a decision maker has to distribute a continuously divisible resource. I now consider a slightly more complicated resource distribution problem.

Double Distribution: Imagine that Kathleen is trying to decide what to do with her life. Just suppose, for sake of simplicity, that Kathleen only has two ethical decisions to make in her lifetime, and that she must make both of these decisions now. Kathleen’s first decision is what she should do with her career, and her second decision is how she should distribute her charitable donations. For instance, Kathleen might choose to work in global health, and to donate as much of her income as possible to animal rights charities. Suppose that Kathleen has positive credences c_health and c_future = 1 – c_health in the moral theories T_health and T_futurerespectively. Under her conditions of moral uncertainty, what is it most appropriate for Kathleen to do?

To apply PRT to this case, I begin by modelling Kathleen as having an initial wealth endowment W, and an initial labour endowment L. L is the amount of time that Kathleen can spend working during her lifetime (I assume, for sake of simplicity, that this value is known with certainty). W is Kathleen’s initial financial wealth, minus the amount of money that she would be required to have now in order to cover her necessary living costs for the remainder of her lifetime. For almost all young people in Kathleen’s position, W will be negative rather than positive. However, I begin by supposing that W is positive, and only later consider the case where W is negative.

As in Distribution, we model the theories T_health and T_future as economic agents, A_health and A_future, whose respective preference structures over outcomes are simply T_health and T_future’s choiceworthiness structures over the corresponding actions. A_health will be initially assigned ownership of c_healthW and c_healthL, and A_future will be initially assigned ownership of c_futureW and c_futureL. If A_health and A_future wish, they can trade and make contracts with each other, and they can also choose to spend their endowments in any of the ways open to Kathleen. For instance, A_future might use her labour endowment c_futureL working for a climate change research team. If this work pays w_climate an hour, then A_future thereby increases her stock of wealth to c_futureW + w_climatec_futureL. A_future might then donate this wealth to climate change charities.

However, suppose that according to the T_future worldview, what the world really needs in Kathleen’s lifetime is more climate change research being done by people like Kathleen. By contrast, according to the T_health worldview, what the world really needs in Kathleen’s lifetime is more donations to global health charities. Under these suppositions, A_health and A_future will almost certainly find it optimal to trade with one another. A_health might sell some of her labour endowment (say L* of it) to A_future, in return for a monetary payment from A_future of c_futureW plus A_future‘s wages w_climate(c_futureL + L*) from working for the climate change research team.⁴² Under these assumptions, the equilibrium outcome might look something like this: A_future will work c_futureL + L* hours in the climate change research team; A_health will work c_healthL + L* hours as, say, a freelance software developer earning w_tech per hour; and A_health will donate W + w_climate(c_futureL + L*) + w_tech(c_healthL + L*) to global health charities. Hence, according to PRT, it would be most appropriate for Kathleen to work c_futureL + L* hours in the climate change research team, and to work c_healthL + L* hours as a freelance software developer, and to donate all of her wealth plus income to global health charities.⁴³

Things can become even more complicated if we make alternative assumptions about the employment options open to Kathleen. Suppose, for instance, that it is impossible for Kathleen to work for only part of her career (i.e.: for anything less than L) in fields that the T_future worldview regards as morally valuable, such as climate change research. In that case, A_future will inherit the same limitations. A_future can only work in climate change research if A_future can afford to buy all of Ahealth’s labour endowment from A_health. A_health, however, might prefer to keep her labour hours than to sell them to A_future at a price of c_futureW + w_climateL, which is the maximum offer that A_future can afford to make. In that case, A_future will not be able to work in climate change research. Suppose that under these conditions, A_future will, just like A_health, favour a plan of ‘earning to give.’ A_future and A_health will both use their labour endowments working as freelance software developers, earning w_tech per hour. A_future will then donate c_futureW + w_techc_futureL = c_future(W + w_techL) to climate change charities, and A_future will donate c_healthW + w_techc_healthL = c_health(W + w_techL) to global health charities. Hence, according to PRT, the appropriate plan would be for Kathleen to work full-time as a software developer, donating c_future of her wealth plus income to climate change charities, and the rest of it to global health charities.

Finally, suppose that W is negative. In that case, A_health and Afuture’s initial wealth endowments c_healthW and c_futureW will likewise be negative. In other words: A_health and A_future will initially be endowed with debts. Both A_health and A_futurewill have to earn enough money – either through working, or through trading with each other – to pay off their initial debts before they can donate any money to charitable causes.

3.5 Trade

Suppose that A_health wants to sell her labour endowment, and that the minimum price A_health is prepared to accept is strictly less than the maximum price A_future is willing to pay. In that case, we will need to invoke some normative solution concept to determine what the price will be. Since some moral theories are not representable by vNM choiceworthiness functions (see §2.3 above), we should adopt a solution concept that – unlike the Nash Bargaining Solution – does not require the agents to have vNM preferences.

I now suggest one such solution concept, that I call Position Maximin.⁴⁴ First, some terminology. An outcome X is Pareto optimal iff there does not exist any alternative outcome Y that every agent weakly prefers, and that at least one agent strictly prefers, to X.⁴⁵ X is individually rational iff every agent weakly prefers X to the disagreement point (defined in §2.2 above). X is an imputation iff X is both Pareto optimal and individually rational.

Define an agent’s position-measured satisfaction with some imputation X as the fraction of imputations that the agent weakly prefers X over.⁴⁶ Thus, an agent’s position-measured satisfaction with some imputation X is an ordinal measure of the desirability to that agent of X (relative to the other available imputations). An agent is positionally worst-off under some imputation X iff her position-measured satisfaction with X is no greater than any other agent’s. Some outcome X is a Position Maximin Solution to some bargaining problem B iff X is an imputation in B, and the position-measured satisfactions of the positionally worst-off agents in B under X are no smaller than the position-measured satisfactions of the positionally worst-off agents in B under any other imputations.⁴⁷ (If there exists more than one Position Maximin Solution for a price dispute in my economic model, then there will simply exist more than one equilibrium, and hence more than one appropriate action.)

The Position Maximin Solution can be understood as the result of an attractive ‘fallback’ procedure for finding a compromise. At the start of this procedure, each agent ‘reports’ the set of imputations S0 that she weakly prefers to every other imputation (in other words: her (joint) favourite imputation(s)). n% of the way through the time allotted for this fallback procedure, each agent reports the set S_n of the imputations that she weakly prefers to at least (100–n)% of all possible imputations. The procedure halts as soon as one or more imputations are being reported by all of the agents. That set of imputations is always identical to the set of Position Maximin Solutions.

§3.6 and 3.8 of this paper illustrate the Position Maximin Solution in cases where the space of imputations is continuously divisible. Here, I illustrate Position Maximin in a case where there are only three imputations. Suppose that there are three agents (A₁, A₂, and A₃) and four possible outcomes (X, Y, Z, and D). The agents’ preferences are as follows, where ≻ denotes ‘is strictly preferred to’:

Table 2: Agents’ preferences

A₁	X≻Y≻Z≻D
A₂	Z≻Y≻X≻D
A₃	Y≻X≻Z≻D

In our bargaining problem, D is the disagreement point. Hence, there are three imputations, X, Y, and Z. Each agent’s position-measured satisfaction with each imputation is as follows:

Table 3: Position-measured satisfaction

	X	Y	Z
A₁	1	2/3	1/3
A₂	1/3	2/3	1
A₃	2/3	1	1/3

Hence, the position-relative satisfaction of the worst-off agent under X or Z is 1/3, whereas the position-relative satisfaction of the worst-off agent under Y is 2/3. Hence, Y is the unique Position Maximin Solution to this bargaining problem.

I also use this case to illustrate the ‘fallback’ compromise procedure that results in the Position Maximin Solution. In this procedure, for the first 1/3 of the time allotted, A₁ reports the set {X}, A₂ reports the set {Z}, and A₃ reports the set {Y}. Then, after 1/3 of the time allotted for this procedure has passed, A₁ reports {X,Y}, A₂ reports {Z,Y}, and A₃ reports {Y,X}. At this point the procedure halts, because Y is now being reported by every agent. Thus, Y is the unique Position Maximin Solution to this bargaining problem.

In this paper, I tentatively adopt Position Maximin as the solution concept in terms of which PRT is defined. However, I do not claim that Position Maximin is necessarily the best solution concept for this purpose. All I claim is that it represents one promising option.⁴⁸ Correspondingly, I do not claim that PRT defined in terms of Position Maximin is necessarily the best possible version of PRT. All I claim is that this version of PRT is superior to the alternative theories of appropriateness outlined in §2.2, and that it hence represents a significant theoretical step in the right direction.

3.6 Contracts

Distributional Jackson: Imagine that some decision maker has 100 units of a resource, each unit of which can be used to purchase a unit of either X, Y or Z. The decision maker has 50% credence in T₁, and 50% credence in T₂. If x, y and z are the total amounts spent on X, Y and Z respectively, then T₁’s choiceworthiness function is 10x + 9y – 10z, and T₂’s choiceworthiness function is –10x + 9y + 10z. In light of her moral uncertainty, what is it most appropriate for the decision maker to do with her 100 resource units? (Just suppose, for sake of simplicity, that this is the last choice situation that the decision maker will face in her lifetime, and that she knows this.⁴⁹ Likewise suppose, for sake of simplicity, that it is impossible for the decision maker to randomise how she will use her resources.)⁵⁰

As before, we begin by modelling T₁ and T₂ as economic agents, A₁ and A₂, whose respective preference structures over outcomes are simply T₁ and T₂’s choiceworthiness structures. A₁ and A₂ are each initially endowed with 50 units of the resource.

If A₁ and A₂ were to each spend their endowment on the good that they most prefer out of X, Y and Z, then A₁ would purchase 50 units of X and A₂ would purchase 50 units of Z. That would leave each theory-agent with a utility of (10 x 50) + (9 x 0) – (10 x 50) = 0. However, if A₁ and A₂ both spent their endowments on Y, then each of them would have a utility of 9 x 100 = 900. In order to achieve this Pareto improvement, A₁ and A₂ can enter into a contract, with each theory-agent promising the other to spend her endowment on Y rather than X or Z.

In fact, this contract is the unique Position Maximin Solution in this choice situation. Any outcome where x and z are both strictly positive is Pareto suboptimal, since it would be a Pareto improvement for ε ≤ x, z less to be spent on each of X and Z, with 2ε more being spent on Y. On the other hand, any outcome where either x or z is zero is clearly Pareto optimal. Hence, an outcome is Pareto optimal iff either x or z is zero. Such an outcome is individually rational iff whichever of x or z is nonzero is no greater than (approximately) 47.37. (If z = 0 , then choiceworthiness according to T2 is ≥ 0 iff x ≤ 47.37. Likewise, if x = 0, then choiceworthiness according to T1 is ≥ 0 iff z ≤ 47.37.) Hence, the set of imputations can be illustrated as follows:

Figure 5: A set of imputations

In Figure 5, an outcome sits on one of the two dashed lines iff it is an imputation. Out of any two imputations, T₁ prefers the imputation that lies furthest to the right, whereas T₂ prefers the imputation that lies furthest to the left. 50% of the imputations lie to the left of (x = 0, y = 100, z = 0), and 50% lie to the right. Hence, (x = 0, y = 100, z = 0) is weakly preferred to 50% of the imputations by both A₁ and A₂. Any point strictly to the right of (x = 0, y = 100, z = 0) is weakly preferred to less than 50% of the imputations by T₂. Likewise, any point strictly to the left of (x = 0, y = 100, z = 0) is weakly preferred to less than 50% of the imputations by T₁. Hence, (x = 0, y = 100, z = 0) is the unique Position Maximin Solution; it is uniquely appropriate for the decision maker to spend all of her resource units of Y. PRT has plausible implications in Distributional Jackson.

3.7: Future-oriented contracts

Theory-agents can also make contracts with each other governing future choice situations. In particular, under PRT, theory-agents will often use future-oriented contracts to maximise their influence over the choice situations that matter most to them.

Priorities: Imagine that at time t₁ a decision maker has 100 units of some resource that she must spend immediately. She will also later receive (at time t₂) another 100 units. At time t₁, each resource unit can be used to purchase a unit of either D or E. At time t₂, each resource unit can used to purchase a unit of either E or F. The decision maker has 50% credence in T₁ and 50% credence in T₂. Suppose for simplicity that she will continue to have these credences forever. If d, e, and f are the total amounts spent on D, E, and F respectively across both time periods, then T₁’s choiceworthiness function is 10d + 2e + f, and T₂’s choiceworthiness function is d + 2e + 10f. In light of her moral uncertainty, what is it most appropriate for the decision maker to do with her resources in each choice situation? (Just suppose, for sake of simplicity, that these are the last two choice situations that the decision maker will face in her lifetime, and that she knows this.⁵¹ Likewise suppose, for sake of simplicity, that it is impossible for the decision maker to randomise how she will use her resources.)⁵²

If A₁ and A₂ were to each spend their initial endowment on the good that they most prefer out of D and E, then A₁ would purchase 50 units of D, and A₂ would purchase 50 units of E (recall that at t₁, D and E are the only options). And then at t₂, after receiving more of the resource, A₁ would purchase 50 units of E, and A₂ would purchase 50 units of F. That would leave each theory-agent with a utility of (10 x 50) + (2 x 100) + 50 = 750. However, if 100 units of the resource were spent on D at time t₁, and 100 units spent on F at time t₂, then each theory-agent would have a utility of (10 x 100) + 100 = 1,100. In order to achieve this Pareto improvement, A₁ and A₂ can enter into a contract, with A₂ promising to purchase 50 units of D at time t₁, and A₁ promising to purchase 50 units of F at time t₂. In fact, this contract is the unique Position Maximin Solution in this choice situation (the proof is omitted, since it is very similar to the one given for Distributional Jackson).⁵³

This example illustrates that under PRT, moral theory-agents will often use future-oriented contracts to maximise their influence over the choice situations that matter most to them. In Priorities, A₂ in some sense sells A₁ the right to choose between D and E, in return for the right to choose between E and F. The latter decision matters more than the former for A₂, and likewise mutatis mutandis for A₁.

Suppose that the decision maker in Priorities does not act appropriately at time t₁. Does this make a difference to what it is appropriate for the decision maker to do at time t₂? I claim that it does not. Contracts between theory-agents concern how resources are used in the economic model of Priorities, which determines which actions are appropriate for the decision maker at times t₁ and t₂. If the decision maker does not purchase 100 units of D at t₁, then she can be legitimately reproached for failing to act appropriately. In virtue of this fact, there is a sense in which A₁ ‘gets what she paid for’ regardless of whether or not the decision maker acts appropriately at t₁, insofar as A₁ gets to determine what is appropriate. Regardless of what the decision maker actually purchases at time t₁, it is still most appropriate for her to purchase 100 units of F at t₂.

3.8: Uncertainty about the future

In many real-world cases, the decision maker is uncertain about which choice situations she will face in the future. I stipulate that in such cases, each theory-agent has the profile of credences over possible futures of the world that is best warranted by the decision maker’s present evidence. Theory-agents will then be able to sign conditionalized contracts with each other, of the form: ‘I agree to give you q units of resource Q now, in return for you agreeing that if a choice situation of type S occurs in the future, then in that situation you will give me r units of resource R.’ A contract of this sort is just a kind of risky outcome, and hence is evaluable by each theory-agent for choiceworthiness in much the same way as any other outcome is so-evaluable. As always, each theory-agent will trade and make contracts so as to maximise choiceworthiness.

Some theory-agents might find it optimal to enter into some rather interesting contracts with each other.

Risk: Imagine that at time t₁, a decision maker has 100 units of some resource that she must spend immediately. Her evidence also suggests there is a 20% chance of her later receiving (at time t₂) another 100 units; otherwise, she will receive nothing. At time t₁, each resource unit must be used to purchase a unit of either G or H. At time t₂, each resource unit must be used to purchase a unit of either I or J. The decision maker has 50% credence in T₁, and 50% credence in T₂, both of which have vNM choiceworthiness functions. Suppose for simplicity that the decision maker will continue to have these credences forever. If g, h, i and j are the total amounts spent of G, H, I and J respectively, then T₁’s choiceworthiness function is 2g + h + i – 16j, and T₂’s choiceworthiness function is g + 2h – 6i + j. In light of their uncertainty about t₂, which contract should the theory-agents A₁ and A₂ (representing T₁ and T₂ respectively) make with each other, if any? (As before, suppose for sake of simplicity that the decision maker will face at most these two choice situations in the remainder of her lifetime, and that she knows this.⁵⁴ Likewise suppose, for sake of simplicity, that it is impossible for the decision maker to randomise how she will use her resources.)⁵⁵

If A₁ and A₂ were to each spend their initial endowment on the good that they most prefer out of G and H, then A₁ would purchase 50 units of G, and A₂ would purchase 50 units of H. And if they received more of the resource at t₂, A₁ would purchase 50 units of I, and A₂ would purchase 50 units of J. That would leave A₁ and A₂ with ex ante utilities (since their utility functions are vNM) of 2 x 50 + 50 + 0.2 x (50 – 16 x 50) = 0 and 50 + 2 x 50 + 0.2 x (-6 x 50 + 50) = 100 respectively. However, if A₁ agreed to purchase 50 units of H at t₁ in return for A₂ promising to purchase 25.21 units of I at t₂, then A₁ and A₂ would have ex ante utilities of 100 + 0.2 x (75.21 – 16 x 24.79) = 35.71 and 2 x 100 + 0.2 x (-6 x 75.21 + 24.79) = 114.71 respectively.

In fact, this is the unique Position Maximin Solution in this choice situation. If A₁ and A₂ together agree to purchase g* units of G and h* units of H at t₁, plus i* units of I and j* units of J if the decision maker receives 100 resource units at t₂, then A₁ and A₂’s ex ante utilities are, respectively u₁ = 2g* + h* + 0.2i* – 3.2j* and u₂ = g* + 2h* – 1.2i* + 0.2j*.

Since g* = 100 – h* and j* = 100 – i*, we can simplify these ex ante utilities as follows:

u₁ = 200 – 2h* + h* + 0.2i* – 320 + 3.2i*

= -120 – h* + 3.4i*

u₂ = 100 – h* + 2h* – 1.2i* + 20 – 0.2i*

= 120 + h* – 1.4i*

Figure 6: Utility functions in an ‘Edgeworth box’

Each dashed diagonal line in Figure 6 is a set of points that all give A₁ the same utility. Likewise, each undashed diagonal line is a set of points that all give A₂ the same utility. A₁ strictly prefers any points below and/or to the right of any dashed line over any of the points on that particular line, and strictly disprefers any points above and/or to the left. Likewise, A₂ strictly prefers any points above and/or to the left of any undashed diagonal line over any of the points on that particular line, and strictly disprefers any points below and/or to the right. Hence, Figure 7 illustrates the set of points that are individually rational (shaded in grey).

Figure 7: Indifference lines in an ‘Edgeworth box’

Figure 8 illustrates the set of points strictly preferred to some arbitrarily chosen individually rational outcome where h* < 100.

Figure 8: Indifference lines in an ‘Edgeworth box’

Since this region is non-empty, no such point is Pareto optimal. By contrast, any outcome where h* = 100 is Pareto optimal, as Figure 9 illustrates.

Figure 9: Indifference lines in an ‘Edgeworth box’

Hence, an outcome is an imputation iff h* = 100 and 64.71 ≤ i* ≤ 85.71. A₁ prefers for i* to be as large as possible, whereas A₂ prefers for i* to be as small as possible. Hence, h* = 100 and i* = (64.71 + 85.71)/2 = 75.21 (midway between 64.71 and 85.71) is the unique Position Maximin Solution. At t₁, it is uniquely appropriate for the decision maker to purchase 100 units of H. A₂ is in some sense insuring A₁ against the possibility of the decision maker receiving another 100 resource units at t₂. What A₁stands to lose should A₂ receive 50 units at t₂ without having signed a contract is greater than what A₂ stands to lose should A₁ receive 50 units at t₂ without having signed a contract.

3.9 Evidence and credence change over time

Suppose that at time t₂ in Risk, the decision maker does receive 100 resource units. What should PRT say is the most appropriate way to use these resources? According to the Obvious Response, the most appropriate way to use these resources is the way specified by the contracts that all of the theory-agents agreed to at t₁. In other words: it is most appropriate for the decision maker to purchase 75.21 units of I and 24.79 units of J.

By contrast, according to the Nonobvious Response, the most appropriate way to use the 100 resource units at t₂ is the way specified by the contracts that all of the theory-agents would have agreed to at t₁, had the decision maker known at t₁ what she knows now (at t₂). The decision maker’s evidence at t₁ suggested that she had a 20% chance of receiving 100 resource units at t₂. At t₂, however, the decision maker has acquired new evidence, because at t₂ she actually has received 100 resource units. Had the decision maker known with certainty at t₁ that she would receive 100 resource units at t₂,⁵⁶ then A₂ would not have agreed at t₁ to the contract described in §3.8 above. Under these evidential conditions, A₁ and A₂’s ex ante utilities at t₁ would have been, respectively:

u₁ = 2g* + h* + i* – 16j*

= -1400 – h* + 17i*

u₂ = g* + 2h* – 6i* + j*

= 200 + h* – 7i*

Figure 10: Utility functions in an ‘Edgeworth box’

As Figure 10 suggests, the unique Position Maximin Solution under the Nonobvious Response is h* = 100 and i* = 55.04. Hence, according to the Nonobvious Response, it is most appropriate for the decision maker to purchase 55.04 units of I, and 44.96 units of J.

The Nonobvious Response is superior to the Obvious Response because it is inappropriate for T₁ to benefit at t₂ from the fact that the decision maker had incomplete evidence at t₁. In other words: it is inappropriate for the decision maker to be governed by the dead hand of her past evidence. The Nonobvious Response is consistent with these intuitively plausible claims, but the Obvious Response is not. For that reason, the Nonobvious Response is superior.

A related question concerns credences over moral theories. Until now, I have been assuming that the decision maker’s credences over moral theories remain constant over time. But what should happen in cases where these credences change over time?

Suppose, for instance, that A₁ agrees to give A₂ some of her resources at time t₁ in return for A₂ giving A₁ some of her resources at time t₂. What should happen if between t₁ and t₂ the decision maker transfers much of her credence in T₁ to some alternative theory T₃? It is most plausible to suppose that this credence shift should diminish A₁’s contractual rights against A₂ at time t₂. If a decision maker has come to substantially repudiate T₁, then A₁ should no longer have extensive influence in determining how it is most appropriate for the decision maker to behave. It is inappropriate for the decision maker to be governed by the dead hand of her past credences over moral theories.

I now show how to honour these intuitions. To determine what is appropriate in some choice situation χn, one should construct an economic model of the whole sequence of choice situations (χ₁, …, χ_n) that the decision maker has faced in her lifetime up to and including χ_n, where in the model of each choice situation χ_i:

(i) Each theory-agent A_j is endowed with a share of the decision maker’s resources in χ_i proportional to the decision maker’s credence at the time of χ_n in the corresponding moral theory T_j.

(ii) Each theory-agent’s body of empirical evidence is the one that she has at the time of χ_n.

(iii) As before:

a. Each theory-agent can spend her resources in any of the ways open to the decision maker in χ_i.

b. Theory-agents can also make contracts with each other, including contracts governing future choice situations (χ_i+1, χ_i+2, etc.).

(iv) Finally, the theory-agents believe that any contracts governing choice situations after χ_n (χ_n+1, χ_n+2, etc.) will be rigorously enforced.

An action is appropriate in x_n iff it is the aggregate of all of the actions performed in χ_n by the theory-agents in some equilibrium of the economic model of (χ₁, …, χ_n) . In other words: what is actually most appropriate in the current choice situation given one’s current credences and evidence is identical to what would be most appropriate in the current choice situation if one had always had those credences and that evidence.⁵⁷

3.10 Choices between discrete options

In introducing PRT, I have been considering cases where the decision maker has to choose how to use an endowment of some continuously divisible resource. By contrast, the existing philosophical literature on moral uncertainty (cf. §2.1 above) is dominated by cases where a decision maker has to choose between two or more discrete options (such as killing the fat man versus letting five people die in ‘bridge’ versions of the trolley problem).

The natural way to extend PRT so as to cover these discrete cases is to stipulate that before each choice situation, each entertained theory-agent A is initially endowed with some c(A)-length segment of the interval [0,1], where c(A) denotes the decision maker’s credence in the moral theory corresponding to A. That segment of [0,1] is like a lottery ticket. A number from [0,1] will be selected randomly, and whichever theory-agent ‘owns’ the segment of [0,1] to which the randomly chosen number belongs will be given the right to perform any one of the actions open to the decision maker in this choice situation – call this the Lottery Rule.⁵⁸ Before the random number is generated, theory-agents can trade their segments of [0,1] between each other, and make contracts. The possibility of contract making means that the equilibrium outcome will sometimes be fully determined even before the random number is selected, either because one theory-agent comes to own every portion of [0,1], or because the theory-agents all promise each other to perform a certain action regardless of which random number is selected. The latter is what will happen, for instance, in many Jackson cases.

In cases where the decision maker is endowed with n indivisible units of some resource, each indivisible unit of the resource should be distributed by its own application of the Lottery Rule – call this iterated application of the Lottery Rule.⁵⁹ As some fixed-size resource parcel becomes more divisible, the number of indivisible units n increases. And as n increases, the probability distribution induced by iterated application of the Lottery Rule tends towards each theory-agent A receiving c(A) of the resource parcel with certainty. This is a desirable result: it shows that the Lottery Rule is entirely consistent with dividing continuously divisible resources between theory-agents in proportion to the decision maker’s credences in the corresponding theories.

4. Evaluating the Property Rights Theory

4.1 Advantages

PRT has several advantages. Firstly, it vindicates Proportionality in Distribution. Secondly, it has no more trouble handling cases where some theories’ choiceworthiness functions are ordinal and non-vNM than it has handling cases where all theories’ choiceworthiness functions are cardinal and/or vNM.⁶⁰ Thirdly, through the mechanism of future-oriented contracts, PRT allows moral theories to have greatest influence (in determining appropriateness) in the particular choice situations that matter most to them.⁶¹

4.2 Moral information

One attractive feature of MEC (a popular rival to PRT) is that it supplies us with an account of the value of moral information.⁶² Imagine that some decision maker knows that she will only face two choice situations in her lifetime. At time t₁ she has to choose whether to pay $w for an infallible oracle to tell her which moral theory is true. After that, at time t₂, she will face Distributional Jackson. At the present moment t₀ the decision maker has 50% credence in T₁ and 50% credence in T₂. According to both T₁ and T₂, spending $w is equivalent to sacrificing w units of choiceworthiness. T₁ and T₂‘s choiceworthiness functions are intertheoretically unit-comparable.

If the decision maker does not consult the oracle at t₁, then purchasing 100 units of Y at t₂ will maximise expected choiceworthiness at 900. If the decision maker does consult the oracle at t₁, then following the plan:

if the oracle endorses T₁ then purchase 100 units of X,
but if the oracle endorses T₂ then purchase 100 units of Z

at t₂ will maximise choiceworthiness at (1000 – w) in each of the two epistemically possible cases. Hence, consulting the oracle will uniquely maximise expected choiceworthiness iff w < 100. According to MEC, at any price less than $100 it is uniquely appropriate to consult the oracle. Such is the value of moral information.

What does PRT imply in this case? Well, if the decision maker does not consult the oracle at t₁, then A₁ and A₂ both know that they will contract with each other at t₂ to purchase 100 units of Y (see §3.6 above). In that case, A₁ and A₂ will each have a utility of 900. Now suppose that the decision maker decides to consult the oracle at t₁. Recall that A₁ is certain that T₁ is true, and that A₂ is certain that T₂ is true. Hence, before t₁ each theory-agent is certain that her preferred theory will be endorsed by the oracle. If T₁ is endorsed by the oracle, then the decision maker will have 100% credence in T₁ at t₂. Therefore, A₁ will receive all 100 resource units, and will spend them all on X, giving A₁ a utility of 1000 – w. Likewise, if T₂ is endorsed by the oracle, then the decision maker will have 100% credence in T₂ at t₂. Therefore, A₂ will receive all 100 resource units, and will spend them all on Z, giving A₂ a utility of 1000 – w. Hence, each theory-agent strictly prefers the decision maker to consult the oracle iff w < 100. According to PRT, at any price less than $100 it is uniquely appropriate to consult the oracle. Just like MEC, PRT supplies us with an account of the value of moral information.

4.3 Complexity

One potential objection to PRT is that it is too complicated, unparsimonious, and difficult to apply. My response to this objection is twofold. Firstly, tu quoque, the best alternatives to PRT are also rather complicated. For instance, the extension of MEC defended by MacAskill, Bykvist and Ord (henceforth: ‘MB&O’) requires considerable ancillary apparatus to handle cases where choiceworthiness is not intertheoretically unit-comparable across all entertained theories.⁶³ Indeed, MB&O themselves report that the entire ancillary apparatus developed over several chapters of their book is in fact intended to handle only a proper subset of all the logically possible forms of comparability.⁶⁴ An exhaustive extension of MB&O’s theory will presumably be even more complicated.

Secondly, many of us are open to the possibility that the correct first-order moral theory is reasonably complicated. In that case, why suppose that the correct theory of appropriateness is any less complex? At the first-order level, a distinction is often drawn between standards of rightness and decision procedures. A standard of rightness determines which actions are right and wrong. However, if a theory’s standard of rightness is difficult to apply, then it will often be supplemented by a decision procedure: a rough heuristic for rightness and wrongness that decision makers can more feasibly be guided by in the real world. One potential strategy for responding to the difficulty-of-application objection to PRT would be to propose a metanormative decision procedure that roughly approximates it. I leave this as a task for future research.

4.4 The Empirical-Normative Analogy

Here is another potential objection to PRT, put in the form of a counterargument:

(i) Normative uncertainty should be handled analogously to empirical uncertainty
– call this the Empirical-Normative Analogy.

(ii) Empirical uncertainty should not be handled analogously to how PRT handles normative uncertainty.

Therefore (iii): PRT is false.

MB&O employ the Empirical-Normative Analogy in their argument for MEC. Since “expected utility theory is the standard way that we should handle empirical uncertainty … maximising expected choiceworthiness should be the standard account of how to handle moral uncertainty.”⁶⁵ Similarly, Tarsney claims that treating normative and empirical uncertainty “differently when we are not forced to is at least prima facie inelegant and undermotivated.”⁶⁶

However, the trouble with the Empirical-Normative Analogy is that there are important differences between normative and empirical uncertainty. First, normative but not empirical uncertainty produces choiceworthiness incomparability. Suppose that some decision maker is 100% certain in some moral theory, and 100% certain in some empirical theory. This decision maker becoming empirically uncertain would not introduce incomparability of choiceworthiness across the different epistemic possibilities. By contrast, I argue in §4.7 that this decision maker becoming morally uncertain would necessarily introduce incomparability of choiceworthiness across the different epistemic possibilities.

Second, whereas the Law of Large Numbers can be invoked to justify expected utility maximisation in at least certain cases of empirical uncertainty, no such justification for MEC is available in cases of moral uncertainty.⁶⁷ Consider, for instance, a case where one can bet over and over again on the rolls of a die. Here, it is clearly legitimate to assume that the die rolls are independently and identically distributed. Under this assumption, the Law of Large Numbers implies that given an arbitrarily large numbers of die rolls, maximising expected utility is overwhelmingly likely to yield greater total utility than repeatedly applying any other policy at each roll of the die.⁶⁸ By contrast, choiceworthiness is not independently distributed across different tokens of any particular type of choice situation. Quite the opposite: if T is right about the choiceworthiness of ϕ-ing in some choice situation x, then T will also be right about the choiceworthiness of ϕ-ing in all other choice situations of exactly the same type as x.

Third, how one should handle empirical uncertainty is also one of the matters about which we are morally uncertain. As I pointed out in §2.3, some moral theories are risk avoidant with respect to choiceworthiness. For instance, suppose that according to T, bringing about some outcome X has choiceworthiness v. If T is risk avoidant, then a 50% chance of bringing about X might be less choiceworthy than bringing about some outcome Y with certainty having choiceworthiness 0.4v. By contrast, vNM moral theories are globally risk neutral with respect to choiceworthiness. I now argue that under conditions of first-order normative uncertainty about how to handle empirical uncertainty, the Empirical-Normative Analogy implies that one has reason to be normatively uncertain about how to handle normative uncertainty, thereby inviting the problem of metanormative regress.⁶⁹

Suppose that some decision maker is certain of

(i) Normative uncertainty should be handled analogously to empirical uncertainty
(the Empirical-Normative Analogy).

Furthermore, this decision maker has strictly positive credence in both

(iv) Empirical uncertainty should always be handled globally risk-neutrally.

and

(v) Empirical uncertainty should always be handled risk-avoidantly.

(i) plus (iv) implies:

(iv*) Normative uncertainty should always be handled globally risk-neutrally.

whereas (i) plus (v) implies:

(v*) Normative uncertainty should always be handled risk-avoidantly.

Thus, on pain of inconsistency, this decision maker should have strictly positive credence in both (iv*) and (v*). If appropriateness depends on one’s uncertainty over propositions like (iv) and (v), then surely it should also depend on one’s uncertainty over propositions like (iv*) and (v*)? After all, uncertainty over (iv*) and (v*) is just a special kind of normative uncertainty: normative uncertainty about how to handle normative uncertainty.

Hence, (iv*) implies:

(iv**) Uncertainty over (iv*) and (v*) should always be handled globally risk-neutrally.

and (v*) implies:

(v**) Uncertainty over (iv*) and (v*) should always be handled risk-avoidantly.

Thus, on pain of inconsistency, our decision maker should have strictly positive credence in both (iv**) and (v**). But since uncertainty over (iv**) and (v**) is itself a kind of normative uncertainty, it should now be clear that there is a problem of metanormative regress.

Rejecting the Empirical-Normative Analogy opens up the possibility that regardless of a decision maker’s credences over (iv) and (v), she should be certain that (for instance) PRT is the correct way to handle normative uncertainty. Rejecting the Empirical-Normative Analogy lets decision makers who are uncertain over propositions like (iv) and (v) avoid the problem of metanormative regress.

4.5 Intertheoretic comparability

A final potential objection to PRT is that it can have implausible implications in certain cases of intertheoretic unit-comparability. Suppose, for instance, that some decision maker has 50% credence in T₁, 50% credence in T₂, and that T₁ and T₂ are intertheoretically unit-comparable. Suppose, furthermore, that T₂* is a hundredfold amplification ⁷⁰ of T₂: if T₂ says that D is x units more choiceworthy than E, then T₂* says that D is 100x units more choiceworthy than E. According to MEC, it makes a big metanormative difference if the decision maker transfers credence from T₂ to T₂*. After such a transfer, it becomes much less frequently appropriate for the decision maker to act according to T₁’s recommendations. By contrast, according to PRT, a transfer of credence from T₂ to T₂* makes no metanormative difference whatsoever.

My preferred response to this objection is to deny that intertheoretic unit comparisons of choiceworthiness are possible.⁷¹ Choiceworthiness unit comparisons make sense only within moral theories, and never between them. Here, I am adopting a firm position on a particularly vexed (and much-discussed) question from the literature on moral uncertainty.⁷² I cannot discuss this question here in anything like the detail it deserves. I shall largely restrict myself to considering two of MB&O’s recent arguments in favour of intertheoretic unit-comparability.

MB&O suggest that there are “many cases where two different moral views intuitively do seem comparable.” For instance, claims like (i) are intuitively plausible:

(i) If animals have rights in the way that humans do, then killing animals is a much more severe wrongdoing than if they don’t.

Similarly, intuitively claims like (ii) seem to be perfectly meaningful:

(ii) Laura used to think that stealing from big corporations was only mildly wrong, but now she thinks it’s outrageous.⁷³

I agree with MB&O’s intuitions about (i) and (ii). But I disagree with MB&O’s interpretations of (i) and (ii) as articulating intertheoretic choiceworthiness comparisons. MB&O interpret (i) as claiming that if animals have rights in the way that human beings do then the wrongfulness of killing animals is much greater than it is if animals don’t have rights.⁷⁴ By contrast, it strikes me as more natural to interpret (i) as claiming that if animals have rights in the way that human beings do, then the wrongfulness of killing animals is a much greater multiple of the wrongfulness of some benchmark wrongful action (such as killing human beings) than it is if animals don’t have rights. This interpretation requires intratheoretic ratio-comparability, but does not require any kind of intertheoretic comparison. (ii) should be interpreted in much the same way.

I now turn to another of MB&O’s arguments in favour of intertheoretic unit-comparability, viz. the argument from “variable-extension cases.” MB&O ask us to consider “two forms of utilitarianism.” These two forms of utilitarianism,

both have exactly the same hedonistic conception of welfare, and they both agree on all situations involving only humans: they agree that one should maximise the sum total of human welfare. They only disagree on the extension of bearers of value. One view places moral weight on animals [– call this version inclusivism]; the other places no moral weight on animals [– call this version exclusivism], and they therefore disagree in situations where animals will be affected. Between these two theories, the intertheoretic comparison seems obvious: they both agree on how to treat humans, and therefore it seems clear that the choice-worthiness difference of saving one human life compared to saving no human lives is the same on both theories.⁷⁵

I disagree with MB&O’s suggestion that these two versions of utilitarianism agree on how to treat humans: exclusivism says that it is always wrong to treat a human badly in order to benefit animals, whereas inclusivism denies this! For that reason, MB&O’s “obvious” comparison claim does not seem obvious to me. On the contrary, one could just as well argue that the difference in choiceworthiness between saving one human life and saving none is greater according to exclusivism than it is according to inclusivism. Inclusivism arguably cares much less about human welfare than exclusivism does, since it denies the exclusivist claim that human welfare is the only game in town. I can see no principled way to adjudicate between this alternative view and MB&O’s “obvious” comparison claim. Variable-extension cases do not provide evidence that intertheoretic comparability is possible.

For all that I have said so far, it might still be the case that there is some privileged way to compare choiceworthiness across inclusivism and exclusivism. Alternatively, there could simply exist many different versions of inclusivism and exclusivism. Perhaps if I₁ is some version of inclusivism, and k > 0, then there exists another version of inclusivism I₂ that is a k-fold amplification of I₁. (According to I₂, the choiceworthiness of any action D is k times the choiceworthiness of D according to I₁.)⁷⁶ I have no knockdown arguments against these possibilities.

Nonetheless, I shall now argue that the balance of evidence presently suggests that intertheoretic unit-comparability is impossible. I have been arguing (contra MB&O) that there are no particular cases where comparability is clearly possible. By contrast, there are some fairly run-of-the-mill cases where comparability is clearly impossible. Consider, for instance, Hedden and MacAskill’s discussions of Average and Total Utilitarianism.⁷⁷ Suppose, for reductio, that

(1-to-1) A unit of total happiness makes the same difference (as measured on some intertheoretic scale) to choiceworthiness according to Totalism as a unit of average happiness makes to choiceworthiness according to Averagism.

(1-to-1) implies that the difference made to choiceworthiness by “increasing the world’s population from 6 billion to 24 billion people at the cost of halving the average happiness level” is 12 billion times greater according to Totalism than it is according to Averagism.⁷⁸ But this is implausible. Could we avoid this implausible result by replacing (1-to-1) with (x-to-1)?

(x-to-1) x units of total happiness make the same difference (as measured on some intertheoretic scale) to choiceworthiness according to Totalism as one unit of average happiness makes to choiceworthiness according to Averagism, where x is some positive constant much greater than 1.

Unfortunately not: (x-to-1) simply causes the reverse problem in cases where, say, the population can be increased by 1 billion at the cost of a 0.1% reduction in average happiness. No unit-comparison proposal will be plausible in all cases. Averagism and Totalism are clearly unit-incomparable. In the absence of any compelling arguments for the possibility of comparability, the simplest hypothesis consistent with current evidence is that intertheoretic unit-comparability is impossible. Hence, my response to the objection to PRT from amplifications is to deny the possibility of intertheoretic unit comparisons.

5. Conclusion

Given the current state of our moral knowledge, it is entirely reasonable to be uncertain about a wide range of moral issues. Hence, it is surprising how little attention contemporary philosophers have paid (until the past decade) to moral uncertainty. In this paper, I have considered the prima facie plausible suggestion that appropriateness under moral uncertainty is a matter of dividing one’s resources between the moral theories in which one has credence, allowing each theory to use its resources as it sees fit. I have gone on to develop this approach into a fully-fledged Property Rights Theory, sensitive to many of the complications that we face in making moral decisions over time. This Property Rights Theory deserves to takes its place as a leading theory of appropriateness under conditions of moral uncertainty.

Acknowledgements: For helpful comments and conversations, I wish to thank Conor Downey, Paul Forrester, Hilary Greaves, Daniel Greco, Shelly Kagan, Marcus Pivato, Michael Plant, Stefan Riedener, John Roemer, Christian Tarsney, and Martin Vaeth. I also wish to thank the Forethought Foundation and the Happier Lives Institute for their financial support.

Appendix: The Asymmetric Nash Bargaining Solution

Let ? denote the set of actions available in some choice situation, and let ? denote the set of entertained theories. For any T ? ? : let CW_T(·) denote some arbitrarily chosen vNM representation of T; let c(T) denote the decision maker’s credence in T; and let d_T denote the choiceworthiness for T of the ‘disagreement point’ (cf. §2.2 above). The Asymmetric Nash Bargaining Solution of the bargaining problem corresponding to this choice situation is:

Elsewhere, I argue that Greaves and Cotton-Barratt’s decision to use the Asymmetric version of the Nash Bargaining Solution is undermotivated ([redacted]). This complication need not concern us here.

References

Benartzi, Shlomo and Thaler, Richard H. 2001. Naive diversification strategies in defined contribution saving plans. American Economic Review, 91.1, 79-98.

Brams, Steven J. and Kilgour, D. Marc. 2001. Fallback bargaining. Group Decision and Negotiation, 10.4, 287-316.

Briggs, R. A. 2019. Normative theories of rational choice: expected utility. In Edward N. Zalta (ed), The Stanford Encyclopedia of Philosophy, Fall 2019.
URL: https://plato.stanford.edu/archives/fall2019/entries/rationality-normative-utility.

Broome, John. 2012. Climate Matters: Ethics in a Warming World (New York, NY: W. W. Norton).

Buchak, Lara. 2013. Risk and Rationality (Oxford: Oxford University Press).

Bykvist, Krister. 2014. Evaluative uncertainty, environmental ethics, and consequentialism. Pp. 122-35 in Avram Hiller, Ramona Ilea and Leonard Kahn (eds), Consequentialism and Environmental Ethics (London: Routledge).

Carr, Jennifer Rose. 2020. Normative uncertainty without theories. Australasian Journal of Philosophy, 98.4, 747-62.

Carr, Jennifer Rose. 2022. The hard problem of intertheoretic utility comparisons. Philosophical Studies, 179.4, 1401-27.

Cohen, Haim, Nissan-Rozen, Ittay and Maril, Anat. Forthcoming. Empirical evidence for moral Bayesianism. Philosophical Psychology.

Congar, Ronan and Merlin, Vincent. 2012. A characterization of the maximin rule in the context of voting. Theory and Decision, 72.1, 131-47.

Conley, John P. and Wilkie, Simon. 2012. The ordinal egalitarian bargaining solution for finite choice sets. Social Choice and Welfare, 38.1, 23-42.

Dietrich, Franz and Jabarian, Brian. Forthcoming. Decision under normative uncertainty. Economics and Philosophy.

Ecoffet, Adrien and Lehman, Joel. 2021. Reinforcement learning under moral uncertainty. Proceedings of the 38th International Conference on Machine Learning, Proceedings of Machine Learning Research 139, 2926-36.

Gracely, Edward J. 1996. On the noncomparability of judgments made by different ethical theories. Metaphilosophy, 27.3, 327-32.

Greaves, Hilary and Cotton-Barratt, Owen. 2019. A bargaining-theoretic approach to moral uncertainty. Global Priorities Institute, working paper 4-2019.

Gustafsson, Johan E. Forthcoming. Second thoughts about My Favourite Theory. Pacific Philosophical Quarterly.

Gustafsson, Johan E. and Torpman, Olle. 2014. In defence of My Favourite Theory. Pacific Philosophical Quarterly, 95.2, 159-74.

Hedden, Brian. 2016. Does MITE make right? Pp. 102-28 in Russ Shafer-Landau (ed), Oxford Studies in Metaethics, volume 11 (Oxford: Oxford University Press).

Hudson, James L. 1989. Subjectivization in ethics. American Philosophical Quarterly, 26.3, 221-9.

Hurwicz, Leonid and Sertel, Murat R. 1999. Designing mechanisms, in particular for electoral systems: the majoritarian compromise. Pp. 69-88 in Murtal R. Sertel (ed), Economic Behaviour and Design, volume 4 of Contemporary Economic Issues (Basingstoke: Palgrave Macmillan).

Jackson, Frank. 1991. Decision-theoretic consequentialism and the nearest and dearest objection. Ethics, 101.3, 461-82.

Karnofsky, Holden. December 13, 2016. Worldview diversification. Open Philanthropy, blog post.
URL: https://www.openphilanthropy.org/blog/worldview-diversification. Accessed March 1, 2022.

Karnofsky, Holden. January 26, 2018. Update on cause prioritization at Open Philanthropy. Open Philanthropy, blog post.
URL: https://www.openphilanthropy.org/blog/update-cause-prioritization-open-philanthropy.
Accessed March 1, 2022.

Kıbrıs, Özgür and Sertel, Murat R. 2007. Bargaining over a finite set of alternatives. Social Choice and Welfare, 28.3, 421-37.

Kihlstrom, Richard E., Roth, Alvin E. and Schmeidler, David. 1981. Risk aversion and solutions to Nash’s bargaining problem. Pp. 65-71 in O. Moeschlin and D. Pallaschke (eds), Game Theory and Mathematical Economics (Amsterdam: North-Holland).

Lockhart, Ted. 2000. Moral Uncertainty and Its Consequences (Oxford: Oxford University Press).

Loomes, Graham. 1991. Evidence of a new violation of the independence axiom. Journal of Risk and Uncertainty, 4.1, 91-108.

MacAskill, William. 2014. Normative Uncertainty. DPhil dissertation. Oxford: Department of Philosophy, University of Oxford.

MacAskill, William. 2016. Normative uncertainty as a voting problem. Mind, 125.500, 967-1004.

MacAskill, William. 2019. Practical ethics given moral uncertainty. Utilitas, 31.3, 231-45.

MacAskill, William, Bykvist, Krister and Ord, Toby. 2020. Moral Uncertainty (Oxford: Oxford University Press).

MacAskill, William, Cotton-Barratt, Owen and Ord, Toby. 2020. Statistical normalization methods in interpersonal and intertheoretic comparisons. Journal of Philosophy, 117.2, 61-95.

MacAskill, William and Ord, Toby. 2020. Why maximise expected choiceworthiness? Noûs, 54.2, 327-53.

Newberry, Toby and Ord, Toby. 2021. The parliamentary approach to moral uncertainty. Future of Humanity Institute, technical report 2021-2.

Nicolò, Antonio and Perea, Andrés. 2005. Monotonicity and equal-opportunity equivalence in bargaining. Mathematical Social Sciences, 49.2, 221-43.

Nissan-Rozen, Ittay. 2015. Against moral hedging. Economics and Philosophy, 31.3, 349-69.

Oddie, Graham. 1994. Moral uncertainty and human embryo experimentation. Pp. 144-61 in K. W. M. Fulford, Grant Gillett, and Janet Martin Soskice (eds), Medicine and Moral Reasoning (Cambridge: Cambridge University Press).

Pivato, Marcus. 2022. Review of Moral Uncertainty. Economics and Philosophy, 38.1, 152-8.

Plant, Michael. July 10, 2022. Wheeling and dealing: an internal bargaining approach to moral uncertainty. Effective Altruism Forum, blog post.
URL: https://forum.effectivealtruism.org/posts/kxEAkcEvyiwmjirjN/wheeling-and-dealing-an-internal-bargaining-approach-to. Accessed July 10, 2022.

Riedener, Stefan. 2021. Uncertain Values: An Axiomatic Approach to Axiological Uncertainty (Berlin: de Gruyter).

Robinson, Pamela. Forthcoming. Is normative uncertainty irrelevant if your descriptive uncertainty depends on it? Pacific Philosophical Quarterly.

Ross, Jacob. 2006. Rejecting ethical deflationism. Ethics, 116.4, 742-68.

Sakovics, Jozsef. 2004. A meaningful two-person bargaining solution based on ordinal preferences. Economics Bulletin, 3.26, 1-6.

Sepielli, Andrew. 2009. What to do when you don’t know what to do. Pp. 5-28 in Russ Shafer-Landau (ed), Oxford Studies in Metaethics, volume 4 (Oxford: Oxford University Press).

Sepielli, Andrew. 2010. ‘Along an Imperfectly Lighted Path’: Practical Rationality and Normative Uncertainty. PhD dissertation. New Brunswick, NJ: Department of Philosophy, Rutgers University.

Sepielli, Andrew. 2013. Moral uncertainty and the principle of equity among moral theories. Philosophy and Phenomenological Research, 86.3, 580-9.

Sepielli, Andrew. 2014. What to do when you don’t know what to do when you don’t know what to do …. Noûs, 48.3, 521-44.

Sepielli, Andrew. 2017. How moral uncertaintism can be both true and interesting. Pp. 98-116 in Mark Timmons (ed), Oxford Studies in Normative Ethics, volume 7 (Oxford: Oxford University Press).

Sepielli, Andrew. 2019. Decision making under moral uncertainty. Pp. 508-21 in Aaron Zimmerman, Karen Jones and Mark Timmons (eds), The Routledge Handbook of Moral Epistemology (London: Routledge).

Sprumont, Yves. 1993. Intermediate preferences and Rawlsian arbitration rules. Social Choice and Welfare, 10.1, 1-15.

Tarsney, Christian J. 2017. Rationality and Moral Risk: A Moderate Defense of Hedging. PhD dissertation. College Park, MD: Department of Philosophy, University of Maryland.

Tarsney, Christian J. 2018. Intertheoretic value comparison: a modest proposal. Journal of Moral Philosophy, 15.3, 324-44.

Tarsney, Christian J. 2019a. Normative uncertainty and social choice. Mind, 128.512, 1285-308.

Tarsney, Christian J. 2019b. Metanormative regress: an escape plan. Unpublished manuscript.

Tarsney, Christian J. 2021. Vive la différence? Structural diversity as a challenge for metanormative theories. Ethics, 131.2, 151-82.

Tenenbaum, Sergio. 2017. Action, deontology, and risk: against the multiplicative model. Ethics, 127.3, 674-707.

Trammell, Philip. 2021. Fixed-point solutions to the regress problem in normative uncertainty. Synthese, 198.2, 1177-99.

Weatherson, Brian. 2019. Normative Externalism (Oxford: Oxford University Press).

Wedgwood, Ralph. 2013. Akrasia and uncertainty. Organon F, 20.4, 484-506.

Wedgwood, Ralph. 2017. Must rational intentions maximise utility? Philosophical Explorations, 20.S2, 73-92.

Endnotes

1
Contact: harry.lloyd@yale.edu. Any critical comments on this working paper would always be gratefully received.
2
J knows exactly what will happen if she donates her money to global health charities. Likewise, she knows exactly what will happen if she donates her money to charities that benefit future generations by fighting climate change. T_health and T_future are competing moral theories, rather than competing empirical theories. A moral theory is a maximally consistent conjunction of propositions about moral facts. For sake of simplicity, I assume in this paper that all decision makers are idealized Bayesian reasoners who have credences over such conjunctions (cf. Cohen, Nissan-Rozen and Maril forthcoming).
3
Greaves and Cotton-Barratt (2019, §7.2) discuss a similar case.
4
In real-world investment decisions, many individuals seem to assume that dividing their savings equally between all of the available options is a sensible response to risk (inter alia Benartzi and Thaler, 2001). Furthermore, in at least some experimental settings, many people divide their resources Proportionally in response to empirical uncertainty (Loomes, 1991). However, on further reflection these choices look more like biases or heuristics than like rational responses to empirical uncertainty. For instance, investors whose financial provider happens to offer four funds in bonds and only one fund in stocks will often invest four-fifths of their savings into bonds and only one fifth into stocks, whereas otherwise similar investors whose financial provider happens to offer four funds in stocks and only one fund in bonds will often invest four-fifths of their savings into stocks and only one fifth into bonds. This is prima facie irrational.

One might worry that the Proportional response to Distribution likewise reflects an irrational bias or heuristic (I thank Martin Vaeth for suggesting this objection.) In response, I report that my personal intuitions in favour of the Proportional response to Distribution are far more robust to reflection than any intuitions that I have in favour of Proportional responses to empirical uncertainty. Moreover, I argue in §4.4 below that normative uncertainty differs in several important respects from empirical uncertainty. An irrational response to empirical uncertainty might be a perfectly rational response to normative uncertainty (and vice versa).
5
Choices between discrete options have thus far dominated the literature on moral uncertainty.
6
MacAskill, Bykvist and Ord 2020, p. 15.
7
MacAskill, Bykvist and Ord 2020, p. 20; see also Bykvist 2014; Sepielli 2014.
8
MacAskill, Bykvist and Ord 2020, p. 20.
9
MacAskill, Bykvist and Ord 2020, p. 20.
10
Gracely 1996; Gustafsson and Torpman 2014.
11
Gustafsson and Torpman’s (2014) modifications need not concern us here.
12
MacAskill, Bykvist and Ord 2020, p. 4. I actually think that MFT is better defined in terms of a slightly different concept, which I call ‘decisionworthiness’ (see [redacted]). We can ignore this complication here.
13
Relatedly, MacAskill, Bykvist and Ord (2020, §2.I) have argued that MFT suffers from a ‘problem of theory individuation’ (see also [redacted]).
14
As with MFT (see n. 12 above), I actually think that MFO is better defined in terms of a slightly different concept to choiceworthiness, which I call ‘decisionworthiness’ (see [redacted]). Again, we can ignore this complication here.
15
Inspired by Jackson 1991.
16
Critics have also outlined money-pump objections to MFO (Gustafsson and Torpman 2014, §2; MacAskill and Ord 2020, §4).
17
MacAskill, Bykvist and Ord 2020, p. 7.
18
Oddie 1994; Lockhart 2000; Sepielli 2009; 2010; Wedgwood 2013; 2017; MacAskill 2014; MacAskill and Ord 2020; MacAskill, Bykvist and Ord 2020.
19
What about cases where choiceworthiness is interval-scale measurable but not inter-theoretically unit-comparable? Perhaps the simplest proposal open to advocates of MEC here is to suggest that one should Maximise Expected Normalized Choiceworthiness (MacAskill, Cotton-Barratt and Ord 2020; MacAskill, Bykvist and Ord 2020, chapter 4; Ecoffet and Lehman 2021). For objections, see Pivato 2022; Gustafsson forthcoming; [redacted].

Secondly, what about cases where one or more of the entertained theories ranks options ordinally rather than cardinally? Perhaps the simplest proposal open to advocates of MEC here is to suggest that one should somehow cardinalize the ordinal theories. After that, one can simply Maximise Expected Normalized Choiceworthiness (MacAskill, Bykvist and Ord 2020, pp. 108-10). For criticisms of and two alternatives to this theory-by-theory cardinalization approach, see Tarsney 2021; [redacted]. Cf. also Tarsney 2019a; Carr 2022; Pivato 2022; Gustafsson forthcoming.
20
Technical note: this definition of expected choiceworthiness is normatively ex post but empirically ex ante – one of four combinatorically possible definitions of expected choiceworthiness. If one restricts MEC to cases where all of the entertained theories have von Neumann-Morgenstern choiceworthiness functions (cf. MacAskill, Bykvist and Ord 2020, pp. 107-8), then these four possible definitions are extensionally equivalent (Dietrich and Jabarian, forthcoming). This complication need not concern us here.
21
Greaves and Cotton-Barratt 2019.
22
One problem with NBT is the problem of scenario individuation: how choice situations are individuated makes a big difference to the theory’s appropriateness judgements. Greaves and Cotton-Barratt (2019, §6) call this the “problem of small worlds”. To overcome this problem, one would have to develop a principled theory of scenario individuation (cf. [redacted]).
23
Greaves and Cotton-Barratt 2019, §3.1.
24
Greaves and Cotton-Barratt 2019, §3.1. I resist this suggestion in n. 39 below.
25
Greaves and Cotton-Barratt 2019, §3.1.
26
Greaves and Cotton-Barratt 2019, §7.2.
27
However, note that it does not support Proportionality as the uniquely appropriate response to Distribution. On the contrary, according to this version of NBT, any lottery having expectation h = 60 is also an appropriate response to Distribution. Greaves and Cotton-Barratt (2019, §7.2) regard this result as implausible, although I am not so sure that I share this intuition.
28
This follows from Greaves and Cotton-Barratt’s (2019, §4.1) “Proposition 1.”
29
Kihlstrom, Roth and Schmeidler 1981.
30
This follows from Greaves and Cotton-Barratt’s (2019, §4.1) “Proposition 1.”
31
Some choiceworthiness function CW( ⋅ ) is an interval-scale measure of choiceworthiness according to some moral theory T iff for any options A, B, C, and D:

(1) CW(A) > CW(B) iff A is more choiceworthy than B according to T; and

(2) CW(A) – CW(B) = k × (CW(C) – CW(D)) iff the difference in choiceworthiness between A and B is k times the difference in choiceworthiness between C and D according to T.

vNM choiceworthiness functions need not satisfy (2).
32
Greaves and Cotton-Barratt (2019, n. 5) explicitly “assume that all moral theories obey the axioms of expected utility theory, in their treatment of empirical uncertainty [i.e.: are vNM].” They admit that “not all moral theories have a structure that is consistent with this assumption,” and that “this is a little awkward, since even if such moral theories seem implausible at the first-order level, ideally we would like our [theories of appropriateness] to apply to agents who have nonzero credence in such theories.” However, Greaves and Cotton-Barratt disclaim that they “do not know how to adapt bargaining theory so that this assumption is not required.”

Explaining a little further: the (Asymmetric) Nash Bargaining Solution is only invariant up to affine transformations of the bargainers’ utility functions. Hence, for NBT to be applicable, (1) the class of affine transformations of the chosen functional representations of the entertained theories’ choiceworthiness orderings must be somehow privileged over any other possible representations of those orderings. Furthermore, (2) the feasible set must be convex in order for the (Asymmetric) Nash Bargaining Solution to satisfy its characteristic axioms. In many cases where one or more of the bargainers have non-vNM preferences, conditions (1) and/or (2) are violated. Restricting the applicability of the (Asymmetric) Nash Bargaining Solution to cases where all of the bargainers have vNM preferences is the generally accepted way to ensure that conditions (1) and (2) are both satisfied.
33
For a defence of this kind of risk weighting, see Buchak 2013.
34
Tenenbaum 2017, p. 675.
35
MacAskill 2016. The Borda Count Theory is designed to handle first-order moral theories that have merely ordinal choiceworthiness functions. See also Tarsney 2019a; MacAskill, Bykvist and Ord 2020, chapter 3; Ecoffet and Lehman 2021; [redacted].
36
Newberry and Ord (2021, §4) suggest that MFT, MFO, and MEC can also be understood in these terms; MacAskill (2016, pp. 979-80) says the same thing about MFT and MFO; see also Ecoffet and Lehman 2021.
37
Since each theory-agent’s preferences are over the space of equilibrium outcomes, each theory-agent cares not just about how she uses her own resources, but also about how the other theory-agents use theirs.
38
Some of these ideas have previously been adumbrated in blog posts by Holden Karnofsky (2016; 2018) and Michael Plant (2022). (This is a case of multiple discovery: I read Karnofsky and Plant’s blog posts after completing the first draft of this paper.)
39
There are at least seven differences between PRT and Greaves and Cotton-Barratt’s NBT:

(1) As I explain in §3.2, the motivating ideas are different. Or at least: PRT’s motivating idea is more specific than NBT’s. Free markets always involve some element of bargaining, but not all bargaining problems take place in free markets. For instance, peace treaty negotiations can be modelled as bargaining problems, even though they are clearly not examples of market interactions. Unlike NBT, PRT is specifically inspired by the market system.

(2) As I explain in §3.5, PRT uses Position Maximin rather than the Asymmetric Nash Bargaining Solution to solve the bargaining problem between theory-agents. For this reason, PRT but not NBT is applicable in cases where one or more of the entertained theories is non-vNM.

(3) As I explain in §3.7, PRT has ‘broader scope’ than NBT, and hence avoids the problem of scenario individuation (cf. n. 22 above).

(4) Relatedly, the revisions to PRT introduced in §3.9 have no parallels in Greaves and Cotton-Barratt’s NBT.

(5) The ‘disagreement point’ used in PRT’s model of resource-distribution choice situations is different from any of the disagreement points proposed by Greaves and Cotton-Barratt (2019, §3.1).

(6) Relatedly, my approach to choosing a disagreement point is very different from Greaves and Cotton-Barratt’s. According to Greaves and Cotton-Barratt (2019, §3.1), one should simply “select some disagreement point such that NBT with that choice of disagreement point supplies a satisfactory” theory of appropriateness. By contrast, PRT’s disagreement point follows from the motivating idea of PRT. In resource distribution cases like Distribution, each theory-agent is endowed with her fair share of the decision maker’s resources. And as I explain in §3.10, in choices between two or more discrete options, each theory-agent is endowed with her fair chance to win the lottery to decide which action is to be performed.

(7) Implicit in Greaves and Cotton-Barratt’s presentation of NBT is the assumption that each theory-agent’s beliefs about what would happen if the decision maker were to perform any action are identical to the decision maker’s own beliefs about this. PRT largely shares this assumption; but it also departs from it in one crucial respect, as I explain in §4.2. This departure allows PRT to provide an account of the value of moral information (which Greaves and Cotton-Barratt do not discuss).
40
Cf. Lockhart 2000, chapter 8.
41
On PRT’s response to Jackson cases, see §3.10 below.
42
I discuss how to determine the value of L* in §3.5 below.
43
I have assumed here that wages are linear in hours worked. In the real world, this assumption is likely to be unrealistic: having two different careers is less efficient than having only one. Relaxing this assumption might, for instance, make it appropriate for A_health and A_future to agree to jointly pursue a single career in software development, with A_health donating her income plus wealth to global health charities, and A_future donating her income plus wealth to climate change charities.
44
Position Maximin generalises the Imputational Compromise solution discussed by Kıbrıs and Sertel (2007) and Conley and Wilkie (2012). It is also closely related to Sprumont’s Rawlsian Arbitration (1993), Hurwicz and Sertel’s Kant-Rawls Compromise (1999), Brams and Kilgour’s Fallback Bargaining (2001), and Congar and Merlin’s Maximin Rule (2012). For an alternative approach to bargaining problems without vNM preferences, see Nicolò and Perea 2005.
45
An agent weakly prefers X over Y iff she thinks that X is at least as good as Y. An agent strictly prefers X over Y iff she thinks that X is better than Y.
46
This definition assumes that there is a privileged interval-scale measurement for any resource that one might be endowed with, unique up to positive affine transformation. For instance, I assume that measuring time in hours, minutes, or seconds is privileged over measuring it in hours squared, or log hours.
47
Unlike the Nash Bargaining Solution, the Position Maximin Solution is defined over the set of possible outcomes rather than over the set of possible utility vectors. That is why the Position Maximin Solution can handle non-vNM preferences (Sakovics 2004).
48
For instance, many will regard Position Leximin as superior to Position Maximin. Fortunately, Position Leximin is extensionally equivalent to Position Maximin in all of the cases considered in this paper.
49
On the relevance of this assumption see §3.7 below.
50
Permitting random lotteries would complicate the PRT analysis but would not alter the key result.
51
On the relevance of this assumption see n. 53 below.
52
Permitting random lotteries would complicate the PRT analysis but would not alter the key result.
53
However, things become much more complicated if we relax the simplifying assumption that the decision maker knows she will not face any further choice situations in her lifetime. If the decision maker believes that she will face additional choice situations after the two described in Priorities, then the outcomes (and hence the imputations) under consideration will have to specify not only what happens in the two choice situations described in Priorities, but also what will happen in the choice situations that will come after them. Any application of PRT to a real world decision problem will have to take such complexities into account. For a response to the worry that this makes PRT implausibly complex, see §4.3 below.
54
On the relevance of this assumption see n. 53 above.
55
Permitting random lotteries would complicate the PRT analysis but would not alter the key result.
56
For sake of argument I assume here that the decision maker could in principle have known this at t₁ (if only she had had sufficient evidence and powers of reasoning).
57
Note that (iv) is not in tension with the Nonobvious Response. (iv) is a feature of the model that determines what is most appropriate in χ_n. Hence, this model ‘goes out of date with’ χ_n. For instance, appropriateness in χ_n+1 is determined by an entirely new model – which itself conforms to (i)-(iv), except with the instances of ‘n’ replaced by instances of ‘n+1′.
58
Cf. Greaves and Cotton-Barratt 2019, §3.1.
59
By contrast, Greaves and Cotton-Barratt’s lottery proposal (2019, §3.1) would distribute all n units through a single winner-takes-all lottery.
60
By contrast, NBT is only applicable in cases where all entertained moral theories have vNM choiceworthiness functions (see §2.3 above). Vis-à-vis MEC on this score, cf. n. 19 above.
61
By contrast, MacAskill, Bykvist and Ord’s preferred extension of MEC to handle cases of intertheoretic unit-incomparability (cf. n. 19 above) does not always give moral theories greater influence over the choice situations that matter more to them ([redacted]).
62
MacAskill, Bykvist and Ord 2020, chapter 9.
63
See n. 19 above.
64
MacAskill, Bykvist and Ord 2020, pp. 5-9; cf. Tarsney 2021. I also argue in [redacted] that precisifying some of MB&O’s proposals requires still further complexities.
65
MacAskill, Bykvist and Ord 2020, §2.III.
66
Tarsney 2021, p. 172; cf. also Sepielli 2010, pp. 75-8; Robinson forthcoming.
67
I am particularly indebted here to Daniel Greco.
68
Briggs 2019, §2.1.
69
On the problem of metanormative regress, see Sepielli 2014; 2017, §6; 2019, §4; Tarsney 2017, chapter 7; 2019b; Weatherson 2019; MacAskill, Bykvist and Ord 2020, pp. 30-3; Trammell 2021.
70
This terminology is from MacAskill, Bykvist and Ord 2020, p. 125.
71
An alternative response is to attempt to modify PRT so as to incorporate sensitivity to intertheoretic unit-comparisons. Future research could investigate the extent to which this response is feasible.
72
See Hudson 1989; Gracely 1996; Lockhart 2000; Ross 2006; Sepielli 2009; 2010; 2013; 2019, §3; Broome 2012, pp. 184-5; Gustafsson and Torpman 2014; Nissan-Rozen 2015; Hedden 2016, §5.2.1; Tarsney 2017; 2018; 2019b, §5.2; Carr 2020, §6; MacAskill, Bykvist and Ord 2020; MacAskill and Ord 2020, §7.iv; Riedener 2021; Gustafsson forthcoming, §5.
73
MacAskill, Bykvist and Ord 2020, pp. 115-7; MacAskill and Ord 2020, §7.iv.
74
MacAskill, Bykvist and Ord 2020, pp. 115-6.
75
MacAskill, Bykvist and Ord 2020, p. 116; MacAskill and Ord 2020, §7.iv; also Sepielli 2019, §3.
76
MacAskill 2019; Sepielli 2019, §3; Tarsney 2019b, §5.2; MacAskill, Bykvist and Ord 2020, §5.VII-VIII.
77
MacAskill 2014, pp. 93-5; Hedden 2016, pp. 108-9; also Broome 2012, p. 185; MacAskill, Cotton-Barratt and Ord 2020, pp. 72-3.
78
Hedden 2016, p. 108.

The property rights approach to moral uncertainty

1. Introduction

2. Alternatives to the Property Rights Theory

2.1 Appropriateness

2.2 Theories of appropriateness

2.3 Proportionality

3. The Property Rights Theory

3.1 The basic idea

3.2 Motivation

3.3 Distribution

3.4: Double Distribution

3.5 Trade

3.6 Contracts

3.7: Future-oriented contracts

3.8: Uncertainty about the future

3.9 Evidence and credence change over time

3.10 Choices between discrete options

4. Evaluating the Property Rights Theory

4.1 Advantages

4.2 Moral information

4.3 Complexity

4.4 The Empirical-Normative Analogy

4.5 Intertheoretic comparability

5. Conclusion

Appendix: The Asymmetric Nash Bargaining Solution

References

Endnotes

Supporting research

Research methods