Cash transfers: cost-effectiveness analysis
- Cash transfers: cost-effectiveness analysis
- Summary
- Outline
- 1. The cost-effectiveness model
- 2. The effect of a cash transfer on the wellbeing of its direct recipient
- 3. Estimated effects of a cash transfer on the individual recipient
- 4. Spillovers: effects on recipients’ household and community
- 5. What is the cost of delivering $1,000 worth of cash transfers?
- 6. Cost-effectiveness of $1,000 spent on cash transfers
- 7. Discussion
- 8. Conclusion
- Appendix A: Other models to explain the impact of cash transfers on SWB
- Appendix B: Monthly CTs total effect example calculation
- Appendix C: Sensitivity analysis
- Appendix D: What is the most cost-effective transfer value?
- Appendix E: Robustness checks
- Appendix F: Research Questions
April 2022: Update to our analysis
This version of the report excluded the intra-household spillovers of cash transfers. Since then, we have updated our analysis to include household spillovers and this decreases the relative cost-effectiveness of psychotherapy from 12x to 9x cash transfers. Our household analysis is based on a few studies, eight for cash transfers and three for psychotherapy. The lack of data on household effects seems like a gap in the literature that should be addressed by further research.
Summary
This report explains how we determined the cost-effectiveness of cash transfers (CTs) using subjective well-being (SWB) and affective mental health (MHa). We define subjective well-being as how someone feels or thinks about their life broadly.1 We further describe what we mean by subjective well-being, and why we believe they are the best measures of well-being, here. We use “affective mental health” to refer to the class of mental health disorders and measures that relate to lower levels of affect or mood (depression and anxiety).2 This differs slightly from the way the term is used clinically to refer to depression, bipolar, seasonal affective disorder, and not anxiety. However, we view this difference as less relevant in practice given that the studies in our sample primarily use measures of depression (CESD10 or GDS-15) or general psychological distress (GHQ12).
Cash transfers (CTs) are direct payments made to people living in poverty. They have been extensively studied and implemented in low- and middle-income countries (LMICs) and offer a simple and scalable way to reach people suffering from extreme financial hardship (Vivalt, 2020).
Specifically, we analyse the cost-effectiveness of sending $1000 using monthly CTs and GiveDirectly CTs (which are typically paid all at once) deployed in LMICs. We fix the total value of money that a recipient receives at $1000, because this is the value of GiveDirectly’s present CTs. These cost-effectiveness analyses form the benchmarks that we use to compare interventions.3 Using cash transfers as a benchmark follows the precedent of GiveWell, a charity evaluator that did pioneering work comparing the cost-effectiveness of interventions in terms of moral value. Recent academic work has also used cash transfers as a benchmark. See McIntosh & Zeitlin (2020) that compared CTs to a USAID workforce readiness program or Haushofer et al., (2020) and Blattman et al., (2017) which compared CTs to psychotherapy.
This report is part of HLI’s search for the most cost-effective interventions that donors and policymakers could fund to increase happiness. We are currently focused on studying micro-interventions in LMICs. To find out more about the wider project see section 2.3 of our research agenda.
This analysis builds on a meta-analysis by McGuire, Kaiser, and Bach-Mortensen (2020), a collaboration between HLI researchers and academics. The meta-analysis gives more background on cash transfers and a much more thorough description of the evidence base. In this cost-effectiveness analysis (CEA) we use the same data to estimate the effectiveness of cash transfers. Specifically we expand on Appendix C of the meta-analysis, which presents a method for estimating the total benefit we expect a recipient of a cash transfer to accrue. We extend that section by predicting the effectiveness of monthly and lump-CTs and adding cost information to estimate the cost-effectiveness of CTs.
We estimate that GiveDirectly transferring $1000 in a lump-sum to people in LMICs leads to an increase in SWB and MHa of 0.92 SDs-years. Monthly CTs delivered by governments increase SWB and MHa by 0.40 SDs per $1000 spent.
Outline
In section 1 we explain the general model for how we estimate the cost-effectiveness of an intervention, which is calculated by dividing the effect a CT has on the average recipient by the cost it takes to deliver a $1,000 CT.
In section 2, we discuss how to estimate the effect of cash transfers. First, we discuss the data we use, then we discuss the models we estimate.
In section 3, we discuss our results. We conclude this section by discussing our estimate for the per person effects of monthly and GiveDirectly CTs on their recipients.
In section 4 we discuss the limited existing evidence on the impact of cash transfers on non-recipients, known as spillover effects. We conclude that there is little existing evidence of negative spillover effects, but some evidence of positive effects on the recipient’s family.
In section 5 we turn to the cost of CTs. We explain how we calculate the total cost to the organization of delivering $1,000 in a CT, most of which comes from the CT itself. Then we summarize the data used to calculate the cost of delivering CTs generally, and for GiveDirectly in particular.
In section 6 we describe the results of our cost-effectiveness analysis and list the other interventions we compare to CTs, briefly summarize the findings, and link to their respective reports. As CTs are the first intervention we have investigated, this part of the document will be periodically updated to reflect the new research we have conducted.
In section 7 we briefly discuss the key uncertainties in our analysis such as spillover effects and effects on mortality. Then we conclude by summarizing our results and outlining ways that further research could reduce the uncertainty in our analysis.
1. The cost-effectiveness model
The cost-effectiveness of an intervention is simply the effect an intervention has divided by the cost incurred to deliver it. Here, we focus primarily on the effect a CT has on the well-being of its recipients (as measured by their SWB or MHa). The evidence of how CTs affect non-recipients SWB and MHa does not indicate, on average, a significant negative effect on the community. While CTs appear to provide a large benefit to the recipient’s household (discussed in section 4.1), the evidence is extremely limited and unbalanced across interventions, so for purposes of comparison across interventions we currently only consider the total effect of an intervention on its direct recipient.
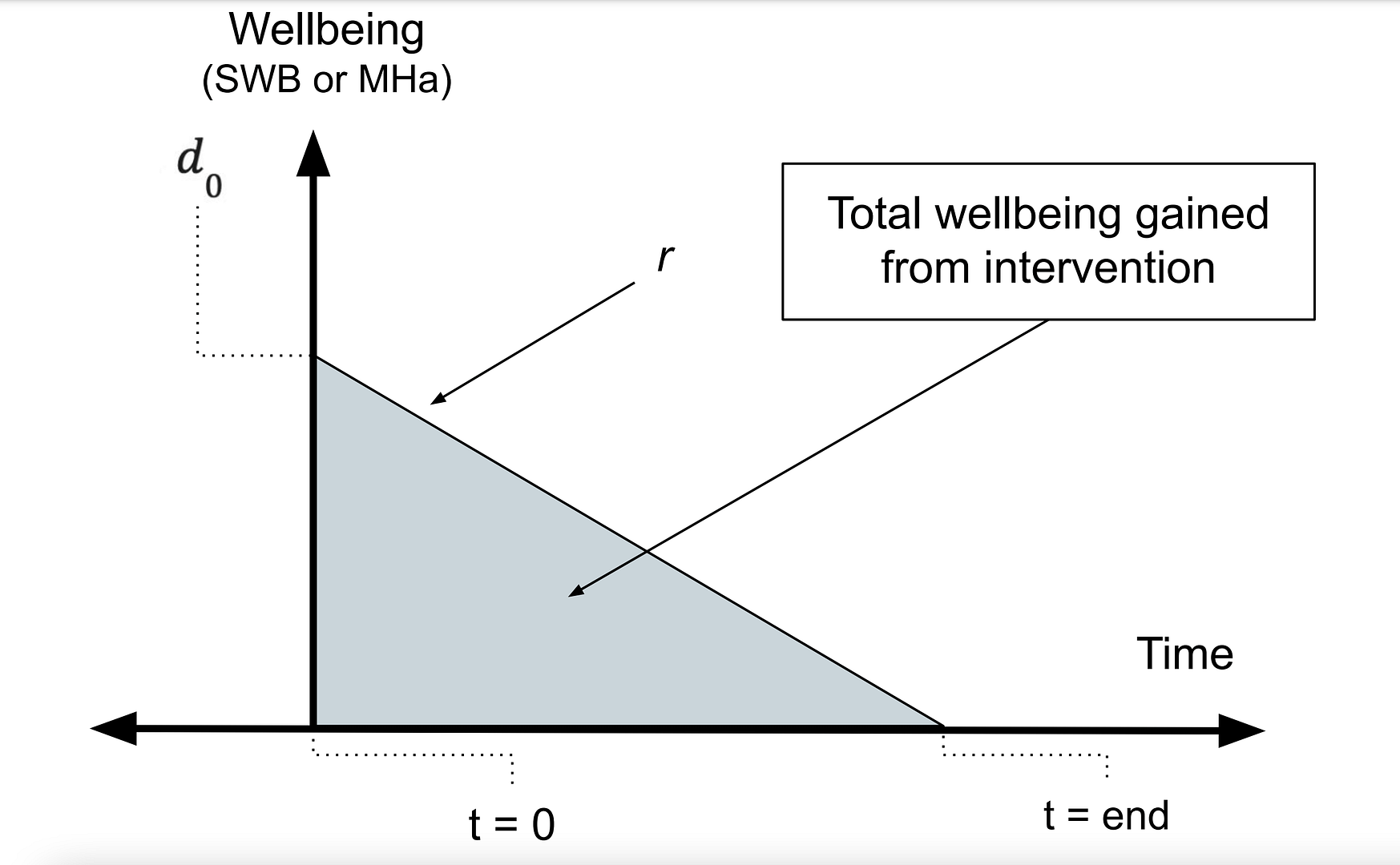
An illustration of the per person effect can be viewed below in Figure 1, where the post-treatment effect (occuring at t = 0), denoted by d0 , decays at a rate of r until the effect reduces to zero at tend. The total effect a CT has on the wellbeing of its direct recipient is the area of the shaded triangle.4 Phrased differently, the total effect is a function of the effect at the time the intervention began (d0) and whether the effect decays or grows (r > 0 , r < 0 ). We can calculate the total effect by integrating this function with respect to time (t). The exact function we integrate depends on many factors such as whether we assume that the effects through time decay in a linear or exponential manner.
Figure 1: Illustration of the total effect of an intervention
Estimating the cost to deliver an intervention is calculated by dividing the total expenses an organization usually incurs5 To put this differently, we take several years’ data of operating expenses into account but put more weight on recent years when making a prediction about future costs. in a given period of time (normally a year) by the quantity of interventions they provided in that year.
In the next section we will explain the data we use to estimate the parameters (![]() , r), which are used to calculate how long the effects last (
, r), which are used to calculate how long the effects last (![]() ).
).
The parameters (![]() ,
, ![]() ) are needed to calculate the total effect an intervention has on its recipient.6 The time the benefits cease is only given by the model in special cases. One case is linear decay if we assume that the effects do not become negative after they reach zero. In a model that assumes exponential decay, the effects last for the rest of the recipient’s life. However, the effects will decay to a point where each additional year yields a benefit very close to zero. In which case tend represents the remaining expected life expectancy of the recipient or the time we assume the effects end, if that occurs earlier than the recipient’s demise.
) are needed to calculate the total effect an intervention has on its recipient.6 The time the benefits cease is only given by the model in special cases. One case is linear decay if we assume that the effects do not become negative after they reach zero. In a model that assumes exponential decay, the effects last for the rest of the recipient’s life. However, the effects will decay to a point where each additional year yields a benefit very close to zero. In which case tend represents the remaining expected life expectancy of the recipient or the time we assume the effects end, if that occurs earlier than the recipient’s demise.
2. The effect of a cash transfer on the wellbeing of its direct recipient
The purpose of this section is to estimate the effect of an average GiveDirectly and government cash transfer. GiveDirectly is one of GiveWell’s top charities for their programme which sends non-recurring lump-payments of $1000 directly to people in low-income countries. Most government CTs employ smaller monthly and bimonthly payments. We use evidence from all lump-CTs to estimate the effect of GiveDirectly’s CTs and monthly CTs to estimate the effect of an average government CT. To be clear, this means we assume that GiveDirectly CTs have similar per dollar effects as the other lump-CTs studied.7 In model 6 of table A.3, we add a variable to indicate if a lump-CT was delivered by GiveDirectly. The results of this model indicate a slightly negative but not statistically significant effect of GiveDirectly delivering the CT (-0.02, 95% CI: -0.14, 0.11).
2.1 Data
The data we use to estimate the total effects of CTs on subjective well-being (SWB) and affective mental health (MHa) is based on McGuire, Kaiser, and Bach-Mortensen (2020) a meta-analysis written by Joel McGuire, a research analyst at the Happier Lives Institute, and two collaborators at the University of Oxford, Caspar Kaiser and Anders Malthe Bach-Mortensen.
The data contains the study-level characteristics (e.g. the treatment effect, dollar value of CTs) extracted from 45 RCTs or quasi-experimental studies of CTs deployed in LMICs. We record the effects on 110 separate measurements of SWB and MHa. That is if a study recorded both the effects on depression and happiness, we recorded both. We included studies that 1) investigate the causal impact of a cash transfer separate from the delivery of other services, 2) report a self-reported measure of MHa or SWB, and 3) are not in a high-income country. We standardized all treatment effects on SWB and MHa using Cohen’s d.8 While this is the conventional way to standardize effect sizes in a meta-analysis, we think it could be worthwhile to check our comparisons using other standardization methods, such as shrinking or expanding all outcomes reported on likert scales to fit a common range e.g., a 0-10 scale. Any positive effect can be understood as a standard deviation (SD) increase in SWB or improvement in MHa. For further details on our selection criteria and data see section 2 of McGuire, Kaiser, and Bach-Mortensen (2020).
The variables most relevant to our analysis are listed below:
- Payment mechanism: whether a CT was paid out in a lump sum (all at once) or a continuous stream of regular payments (monthly or bimonthly).
- Years since CT began: the time of the follow-up survey recorded in years since the CT began. For lump-sum CTs this is also approximately the time since the CT ended.
- Value: the value of a cash transfer in terms of purchasing power parity adjusted US dollars (PPP USD).9 Our data also includes a variable that captures the value of a CT relative to previous income. We don’t use this variable because it doesn’t allow us to estimate the effect of GiveDirectly’s usual $1000 CT. Due to inconsistent reporting, constructing this variable requires more imputation and is noisier as a consequence.
- Measure of subjective wellbeing or affective mental health: the outcomes we use to measure the effectiveness and impact of cash transfers.
Years since CT began and the value of the cash transfer allows us to model the effect, over time, of transferring $1000 to someone in a LMIC. The dollar value for a lump CT is the total amount of money sent. For monthly CTs, value is the size of the transfer received each month. We aggregated monthly and lump CTs in McGuire, Kaiser, and Bach-Mortensen (2020), but here we disaggregate them to make predictions about CTs of different kinds. This has a consequence of reducing the statistical power of our analysis.
The payment mechanism is important for two reasons. Firstly, lump-sum and monthly CTs have different interpretations for their “value” and “years since CT began” variables. In 29 out of 32 monthly CTs studies, recipients were still receiving transfers at the time of the latest follow-up. This changes the interpretation of the benefit’s decay through time (r). Decay in the effects of a monthly CT over time is more consistent with adaptation to a higher income. In contrast, decay in the effectiveness of a lump-sum CT is more consistent with depleting the funds provided by the CT. However, if lump CTs are invested prudently, i.e., to purchase a metal roof, then they both lead to persistently higher standards of living, albeit through different means.
Secondly, the payment mechanism and type of organization deploying the CT are correlated. Of the 45 CT studies we consider, 29 (out of 32) monthly CTs are delivered by governments and 8 (out of 13) lump-sum CTs are delivered by GiveDirectly. This high correlation between these two variables restricts our ability to untether the influence that payment mechanisms and organization type have on a CT’s effectiveness.
We’ve already introduced the constructs of subjective wellbeing and affective mental health. In our data we include measures of how people answered questions such as “How happy are you (on a scale of 0 to 10)?” or responded to MHa questionnaires like the CESD, a twenty item depression questionnaire. Our main results are the pooled differences in responses to these questionnaires between treatment and control groups (which received no intervention at any time). We show the disaggregated results by measure class in Appendix E, Table A4.
2.2 Summary of data
In Figure 2, shown below, we illustrate the distribution of several variables relevant to our analysis. First, we show the distribution of effect sizes for every outcome standardized using Cohen’s d. To the right of that, we show the breakdown of outcomes by their type of measure. The most common outcome measure is depression or psychological distress followed by life satisfaction and then happiness. The other outcome measures are classified as combinations of multiple measures.
Interestingly, there are few CT studies that follow-up within a year after the CT began. RCTs on many other topics, such as psychotherapy, follow-up within a year after the intervention ended but do not follow-up after that. In the last panel, we show that most CTs are deployed by governments, almost all GiveDirectly CTs are paid out in lump-sum CTs, and there are not many other CTs deployed by academics or NGOs outside of GiveDirectly.
Figure 2: Summary plots of the data

Note: D = depression and distress, HP = happiness, LS = life satisfaction, OtherSWB = other measures of SWB that are not LS and HP, including indices that combine both HP and LS. PWBindex = an index combining both SWB and MHa measures. Other = other measures of MHa that are not depression or distress, such as anxiety or indices that capture depression, stress and anxiety.
Next, we show the average income levels of the samples we study, broken down by country. Most studies take place in Africa and their samples consist of people with very low incomes. Average income in all samples, except Blattman et al.’s 2017 study in Liberia, fell below the country’s poverty level (as defined by the country).
Figure 3: Average income level of samples studied

Note: The width of the bar plots is proportional to the number of studies conducted in that country (Kenya had the most CTs studied).
2.3 Model choice
We choose a linear model (shown below as equation 1) to estimate how the effects change through time and how much wellbeing increases in relationship to the value of the CT because a linear model (somewhat surprisingly10 We say surprisingly because we share the conventional belief that there are diminishing returns to income. ) fits the data best compared to all other specifications we considered.11 We assessed goodness of fit based on whether it had a higher R2 and lower AIC and BIC statistics. We also considered a linear model without an intercept, models that assumed a quadratic or logarithmic relationship between SWB-$value and a model that assumed that the benefits decay exponentially. We discuss these models and how much of a difference they would have made if we used them in Appendix A.
![]()
2.4 Expectations
We expect our model to predict that receiving more money makes recipients happier and we expect the effects to decay through time. Decay seems reasonable to expect because it appears that people adapt to changes in their circumstances (Luhmann et al., 2012). We also expect the benefit of CTs to stem from increased consumption, and that CT recipients will eventually spend all the money they receive.
3. Estimated effects of a cash transfer on the individual recipient
First, we present visually in Figure 4 the simple correlational relationship between the effect of a CT, its dollar value and the time since the CT began. As we expect, the effects decay through time and grow when CTs are more valuable.
Figure 4: The effect of CTs through time and relationship to value of the transfer

Note: These results only display the bivariate relationship between value, time, and the effect. They do not control for the other variables.
Next, we describe our models for estimating the effectiveness of lump-sum cash transfers (model 1) and monthly cash transfers (model 2) descriptively in Table 1. In Table 1, we show the exact slope of the relationship estimated by model (1). Next, we discuss the results row by row.
Table 1: Explaining the wellbeing effects of CTs using value and time since the CT began
| Dependent variable: SDs of change in SWB and MHa | ||
| Model 1: Linear models of lump-CTs effectiveness | Model 2: Linear model of monthly CTs effectiveness | |
| intercept | 0.120 (0.038, 0.203) |
0.086 (0.04, 0.132) |
| $PPP value | 0.059 (-0.029, 0.146) |
0.613 (0.193, 1.033) |
| Years since CT ended | -0.028 (-0.04, -0.017) |
-0.014 (-0.023, -0.004) |
Note: $PPP are in units of thousands, 95% confidence intervals are shown below the parameter estimate.
In Models 1 & 2 there is a positive, sizable, and statistically significant intercept. The intercept can be interpreted as the predicted effect of a cash transaction at the time of the first transfer for a cash transfer that has no monetary value or condition. This intercept taken literally implies that a $0.01 lump-sum CT is about half as effective as a $1,000 CT, and thus wildly more cost-effective. However, we do not think such an interpretation is warranted.12 We think that receipt of a government CT can be related to accessing other welfare services. This appeared to be the case in Ghana (Handa et al., 2014) and China (Han & Gao, 2020). Our data does not include any CTs below 10% of recipients pre-transfer household income and the earliest follow-up occurs around a year after the CT began. That means our intercept is the result of an out-of-sample prediction produced by linear extrapolation, which is unreliable.
The next row of the table shows the expected impact of increasing CT size by $1,000. For lump-sum CTs (model 1), a CT that’s $1,000 (PPP) larger can be expected to have an additional effect of 0.06 SDs of SWB and MH. For monthly CTs, an additional $1,000 (PPP) every month is associated with a 0.6 SDs improvement in MH. Recall that the coefficients are not comparable because monthly and lump-CTs are in different units ($total vs. $per month).
Note that the relationship between money granted and SWB plausibly depends on the recipient’s baseline income. We demonstrated in Figure 2 that the recipients of CTs we observe have low incomes, but there are a few samples that are relatively better off by $500-$1,000 a year. If we remove those richest samples (or simply control for baseline household income) it does not change the results much. We give more detail in a footnote.13 Removing the samples with incomes of more than $4,000 a does not change the total effect of lump-CTs but increases the total effect of monthly CTs by 0.05 SDs. Controlling for baseline income increases the total effect of both lump and monthly CTs by 0.07 SDs (see models 2 and 3 in Table A.2 and models 1 and 2 in Table A.3).
The third row of Table 1 gives the decay rate. After every year since the initial receipt of the cash transfer we can expect the benefit of lump-sum CTs to decay by -0.028 SDs,14 Observing the first panel of Figure 4, it seems like the decay rate of lump-CTs could depend on an unusually long follow-up (Blattman et al., 2020). If we remove this study it leads to the decay rate decreasing from -0.28 to -0.26 and the total effect increases from 1.05 to 1.10. and monthly CTs to decay by -0.014 SDs.15 In McGuire, Kaiser, and Bach-Mortensen (2020), we did not find a similar magnitude difference in decay rates because we controlled for a large number of other variables when testing for a significant interaction, which makes a comparison between these results difficult.. The models imply that monthly CTs decay more slowly than lump-sum CTs. This seems reasonable because recipients of monthly CTs are still receiving payments. We consider how monthly CTs decay after the transfers end in section 3.2.
3.1 Does it make a difference to the effect which outcomes we use?
In our data we include information on whether an outcome was a measure of MHa (i.e., depression) or SWB (i.e., happiness, or life satisfaction). The effects appear larger when measured using measures of SWB (by 0.01 and 0.12 SDs-years for monthly and lump CTs).16 These absolute increases correspond to a 2% and 13% increase relative to if all outcomes were pooled, see model 4 in Table A.2 and model 3 in Table A.3. If we disaggregate further, we find that the total effects shrink for lump-CTs and grow for monthly CTs. The total effect on HP measures is 0.42 SDs (84%) higher for monthly CTs but lower by -0.66 (63%) for lump-CTs. For LS the differences are smaller: the effects are higher by 0.04 SDs (48%) in monthly CTs but lower by -0.09 SDs (8%) in lump CTs. We think this is probably due to noise because we do not have a reason to believe that the delivery mechanism should influence questionnaire response. But we keep the outcomes pooled and implicitly treat them as equally informative to maximize the data we can use. To see a full list of the measures of SWB and MHa included, see Table 1 of McGuire, Kaiser, and Bach-Mortensen (2020).
3.2 Calculating the total effects of CTs based on model results
With the results presented in Table 1 we have everything we need to calculate the total effects lump-sum CTs have on their recipients’ SWB and MHa. To calculate the total effects of monthly CTs requires that we impute how monthly CTs decay once the CT has finished. We assume that the benefit of monthly CTs will start to decay at the same rate as lump-sum CTs once they have ended.17 We think this is reasonable because the decay rate for lump-sum CTs represents the best evidence for what happens to the effects of a CT after payments have ceased. But because we’re uncertain about this point we apply a subjective 40% increase factor to the existing CI around the decay produced by the lump-sum CT model. We discuss in section 6.2 and Appendix C how sensitive the total effects are to this uncertainty. We find that they are not. Variation in the post-transfer decay rate of monthly CTs only explains 2% of the estimated uncertainty in the total effects of monthly CTs. Currently, we implement no discount rate for wellbeing gained in future years. We illustrate the total effect and decay of lump-sum CT and monthly CTs in Figure 5 below.
Figure 5: Effect of $1,000 paid in lump-sum and monthly CTs through time

Note: Assumes linear decay that stops at zero, where monthly CTs decay at the rate of lump-sum CTs after payments.
Finally, we can estimate the 95% confidence interval of the total effects by running a simple Monte Carlo simulation where each calculation is run 5,000 times. In this simulation, we assume each parameter18 In addition to simulating the regression parameters, we assign a range of values to the payment size for monthly CTs. We do this only for monthly CTs because we are uncertain about their true value, however we know that GiveDirectly sends $1000 CTs. For $value of the monthly CTs, we allow the amount to vary symmetrically around the average CT size $22.5 by ten dollars (the range most monthly transfers fall in) while fixing the total value of transfers sent at $1,000. Recall that, for linear models, tend is determined within the model. So the distribution of tend is simply a function of the decay rate and effect immediately after receipt. that we’ve discussed (![]() , r) is drawn from a normal distribution centered on its point estimate with its variance derived from the confidence intervals our regression models produce. That is, we convert the 95% CI’s estimated from study-level data we’ve collected to the 5th and 95th percentiles of the simulated distribution. For example, the distribution for the annual linear decay rate for monthly CTs will have a mean of -0.014 and a normal distribution with its 5th and 95th percentile of -0.023 , -0.004 (these are the CI’s given in model 2 in Table 1).
, r) is drawn from a normal distribution centered on its point estimate with its variance derived from the confidence intervals our regression models produce. That is, we convert the 95% CI’s estimated from study-level data we’ve collected to the 5th and 95th percentiles of the simulated distribution. For example, the distribution for the annual linear decay rate for monthly CTs will have a mean of -0.014 and a normal distribution with its 5th and 95th percentile of -0.023 , -0.004 (these are the CI’s given in model 2 in Table 1).
3.3 Example calculating the total effects using point estimates
In this section we explain how we used the model results to calculate the effects of a lump-sum CT. We walk through the calculations for monthly CTs in Appendix B.
If we assume that the decay stops at zero, then the total effect of a CT is equal to the area of the triangle, or ½ ![]() * tend, i.e. one half of the post-intervention effects multiplied by the duration that the effects last. Note that this is only applicable when assuming linear decay.
* tend, i.e. one half of the post-intervention effects multiplied by the duration that the effects last. Note that this is only applicable when assuming linear decay.
First, we calculate the effect of a $1,000 CT in regular (not-PPP) USD predicted to occur at the time of receipt (![]() ). A $1,000 CT is worth $2,100 in terms of PPP for the average country in our sample. So the post-intervention effect is
). A $1,000 CT is worth $2,100 in terms of PPP for the average country in our sample. So the post-intervention effect is ![]() = intercept + (0.06* $value in thousands) = 0.12 + ( 0.06 * 2.1) = 0.24 SDs.
= intercept + (0.06* $value in thousands) = 0.12 + ( 0.06 * 2.1) = 0.24 SDs.
The time when the effect of the CT ends can be calculated by dividing the effect at the time of the receipt (![]() ) by the decay rate r. Both of these are given in Table 1. tend = |
) by the decay rate r. Both of these are given in Table 1. tend = |![]() / r| = |0.24 / – 0.03| = 8.6 years. So the total effect of a $1,000 lump-sum CT is ½ * 0.24 * 8.6 = 1.05 SDs-years. Note that this result differs from the average estimated in the simulation (shown in Table 2 below). We explain why in a footnote.19 An alternative and more compact way of expressing the total effect is to write it as
/ r| = |0.24 / – 0.03| = 8.6 years. So the total effect of a $1,000 lump-sum CT is ½ * 0.24 * 8.6 = 1.05 SDs-years. Note that this result differs from the average estimated in the simulation (shown in Table 2 below). We explain why in a footnote.19 An alternative and more compact way of expressing the total effect is to write it as ![]() 2/-2r. From that expression we can see that the difference between our simulation and a calculation based on expected values is due to Jensen’s inequality. This is because E(d02/-2r), which is what estimate in our simulations, is not equal to E(d0)2/2E(-r) The total effect of cash transfers on the recipient is summarized in Table 2 below.
2/-2r. From that expression we can see that the difference between our simulation and a calculation based on expected values is due to Jensen’s inequality. This is because E(d02/-2r), which is what estimate in our simulations, is not equal to E(d0)2/2E(-r) The total effect of cash transfers on the recipient is summarized in Table 2 below.
Table 2: Total effect of cash transfers
| Total effect in SDs-years of SWB and MHa per $1,000 in CTs | |
| Lump-sum CTs | 1.09 (0.329, 2.08) |
| Monthly CTs | 0.50 (0.216, 0.920) |
Note: The 95% confidence interval is shown below the estimated effect.
Notably, the estimated total effect of a $1,000 lump-sum CT is about twice as large as the effect of $1,000 transferred in $20 ($10 to $30) increments across 50 (33 to 100) months by (mostly) governments. The difference in total effects is 1.09 for lump-CTs compared to only 0.50 SDs-years increase in SWB and MHa for monthly CTs. This at first seems like a suspiciously large difference since we do not think a priori that giving people of similar means the same sum should have dramatically different effects.20 In McGuire, Kaiser, and Bach-Mortensen (2020) we do not find a statistically significant difference in the initial effects of monthly and lump CTs. The differences in the total effects do not appear significant here either, since the 95% confidence intervals overlap. We explain which variables are driving the difference in a footnote.21 This difference is driven most by a difference in the intercept, followed by a difference in the effect of the CT value. The decay is slower in monthly than lump CTs so this does not explain lump-CTs advantage. Monthly CTs do have a shorter duration because duration is determined not by the decay rate, but by the decay rate of lump-CTs (for after the transfer ends) and the size of the monthly transfer e.g, a $100 transfer would spend $1000 in ten months. We explain the differences by seeing how much of the gap in effects closes when moving the point estimate of a monthly-CTs variable from its expected value to the upper bound of its estimated CI. If we assume the upper bound of the intercept, the gap closes 52%, for the transfer-period decay, 30%, for $value, 17% and for the post transfer decay 8%.
There are a few possible explanations for the difference. One explanation is that lump-sum CTs can be invested more profitably, leading to higher total consumption and benefit. However, monthly CTs could lead to smoother consumption and that could benefit the recipient. Differences in household income may be another reason for the difference in predicted total effects between CT delivery mechanisms. Households in lump-sum CT studies have around 10% lower incomes and household sizes that are about one person larger.
The second explanation is that most lump-CTs are by academics or GiveDirectly. CTs are more reliable than Government CTs. Since the value of the CT that the recipient received was not recorded in most studies, we used the value a recipient was intended to receive. It seems plausible that there’s more leakage in government CTs22 In general, if measurement error is larger for monthly CTs than for lump-sum CTs, then the effectiveness of monthly CTs will be underestimated relative to lump-sum CTs. This is because estimated coefficients on explanatory variables that are measured with greater error are relatively more biased towards zero. This issue would be exacerbated if, as we’re concerned, the measurement error overestimates the amount of money monthly-CT recipients receive. than with GiveDirectly. One reason for the leakage is that many governments in LMICs suffer from corruption, while GiveDirectly is a respected charity. A second reason is that many government CTs require that an individual travel in person to a collection point while GiveDirectly CTs are transferred automatically using the mobile banking platform M-Pesa. GiveDirectly also provides cell phones and a bank account to recipients without it.23Although they take the value of the phone out of the transfer, this could plausibly provide an additional benefit to the recipient. Haushofer & Shapiro (2016) acknowledge that the treatment effect “is thus a combination of cash transfers and encouragement to register for M-Pesa.”. It’s unclear if their design or data collection permits them to estimate the effects of registering for M-Pesa on SWB. When we reviewed their data (it’s open access), it did not appear possible.
As we previously mentioned, we only have a small sub sample of studies we can use to separate the influence of payment mechanisms from the type of implementing organization. However, if we estimate the effect of deployment organization we find that GiveDirectly lump-CTs are estimated to have a lower but n.s. initial effect of -0.02 SDs (95% CI: -0.14, 0.11) compared to lump-CTs administered by academics or governments.
In the next section we discuss some ways that the total effects could be larger (or smaller) when we account for the effects CTs have on non-recipients: people who didn’t receive a cash transfer.
4. Spillovers: effects on recipients’ household and community
Our analysis doesn’t include the effects of a CT on non-recipients. This is due to the limited evidence, but in principle these spillovers should be included. The recipient is plausibly not the only person impacted by a cash transfer. They can share it with their partner, children, friends or neighbours. Such sharing should benefit non-recipients’ well-being. However, it’s also possible that any benefit non-recipients receive could be offset by envy of their neighbour’s good fortune. First, we discuss the evidence that finds positive intra-household spillovers. After that, we turn to community spillovers where we discuss the null results of a small meta-analysis of community wide spillover effects.
4.1 Evidence of household spillovers
We frame the direct evidence of a CT on recipients’ household members in terms of the share of benefit the household member received compared to the recipient. We found four studies that measure the impact of a CT on both recipients and members of the recipients’ household. In every study, the effects on other household members are all positive. In two studies, the benefits to the household member are smaller than the benefit of the direct recipient and in the other two studies they are larger.24 Other studies may allow for the estimation of household effects from CTs, but we have not confirmed that their samples overlap. Kilburn et al. (2018), Molotsky & Handa (2021), and Angeles et al. (2019) all take their samples from the Malawi Social Cash Transfer. The first two deal primarily with adults while the third analyses the adolescent sample. Similarly for the Kenyan CT-OVC, Handa et al. (2014) comes from an adult sample, while Kilburn et al. (2016) is based on an adolescent sample. These two pairs of adult and adolescent samples, since they are the children or wards of the adults, could be used to approximate household spillover effects if we were given more information. A further complication is that these sets of studies use different follow-ups across adult and adolescent samples. Ideally we would compare effects on adults and children at the same follow-up.
In Ohrnberger et al. (2020) the average benefit for MHa of the child support grant in South Africa for other household members was 63% that of the recipient. Baird et al. (2013) found that the spillover effect on the siblings’ MHa of a young woman who received a CT was 40% as beneficial for MHa.
In Ozer et al. (2009; 2011) the benefits to the child’s MHa are 1.75 times the benefit to the mother. In Haushofer et al. (2019) the benefit the recipient’s partner receives is 1.48 times the benefit received by the recipient. A simple average of these results indicates that the expected effects of a CT on other household members that aren’t the direct recipients are roughly equal to the benefits accrued to the recipient themselves (1.07x). If taken seriously, this could suggest that CTs are typically distributed equally within households.25 If CTs have equally large effects on other household members then we can calculate the total effect of a CT on the recipient and their household by multiplying the total effect on the average recipient by the expected household size.
In addition to improving the lives of the CT recipients’ households, CTs may extend the life of household members. There is some preliminary empirical evidence that suggests that parents are more likely to provide additional health interventions26 McIntosh and Zeitlin (2020) found a GD lump-sum cash transfer of $532 (that cost $567 to deliver) reduced child mortality in the year after the CT by around 1 percent. If we assume their findings generalize, then for every $1,000 spent on GD CTs, there are 0.018 lives saved. This could entail a large additional benefit depending on one’s view of the badness of death (HLI, 2020). For instance, if we held the same assumptions as we do in our report on moral weights, this would imply 1.3 (95% CIL: 0.11 to 2.2) additional SDs of well-being gained from CTs for someone with a complete belief in deprivationism. In at least one study, a UCT paired with health education led to an increase in the likelihood the child was vaccinated for tetanus and given preventative treatment against malaria outcome (Briaux et al. 2020). to their children in response to receiving a CT.
We defer incorporating these household spillovers into the total effects of cash transfers. This means we are implicitly assuming that the spillover effects are proportional across interventions. That is, if the household benefits 50% as much as the recipient in one intervention, that’s also the case in the other interventions. It’s unclear how reasonable this assumption is. We will revisit this issue after we have reviewed the empirical evidence27 Gathering more evidence on how interventions trigger the provision of further interventions warrants its own research project. on whether spillover effects appear differential across other interventions, such as psychotherapy.
4.2 Evidence of community spillovers
In McGuire, Kaiser, and Bach-Mortensen (2020) we identified four CTs which assessed spillover effects on non-recipients of CTs (total sample size = 10,155). These studies assume that spillover effects are limited to the geographic proximity of the CT recipients. Under this assumption the authors estimated spillover effects by adding an additional control group that was in a village distant from the CT recipients and thus presumed to be free of any spillover effect. The within and across village spillover effects were then calculated by comparing the difference in SWB between non-recipients nearer and farther from the CT recipients.
Four CTs (total sample size = 7,501), assessed the within-village spillovers, and found that the effect was a decrease of -0.009 SDs of SWB per non-recipient (95% CI: -0.098, 0.081), at an average of 1.6 years after the CT began. Note that if the ratio of non-recipients to recipients is high enough, this effect could be large enough to reduce the effectiveness of CTs. It’s unclear what this ratio of recipients to non-recipients would be on average for GiveDirectly villages or for government CTs.
One CT study (Egger et al., 2020) also included across-village spillover effects and found that the average across village spillover effect caused a 0.07 (95% CI: -0.004, 0.15) increase in SWB and MHa. We therefore do not interpret the evidence as suggesting that there are significant within or across village spillover effects. The magnitude of community spillover effects will depend on the ratio of recipients to within and across village non-recipients who experience the spillover effects. We are currently unsure about the value of this ratio in practice.
We do not include these spillover effects in the main analysis because the evidence is slim but the effects on other household members could influence the relative effectiveness of interventions. We discuss this further in a footnote.28 In a simulation (using Guesstimate), we performed a ‘back of the envelope’ calculation where we made the following assumptions: 1) the ratio of benefits to the household relative to the impact to the direct recipient were between of 50% and 150% (95% percentiles of a normal distribution), and 2) the non-recipient household size was 3.7. Under these assumptions, including the household effect would increase the total effect substantially to 4.1 SDs (95% CI: 1.1 to 8.7). To estimate the impact of community spillovers we assumed 3) there were between 1 and 10 non-recipients in the community for every direct recipient, and 4) that the spillover effects lasted between 1 and 6 years. Given these assumptions, the negative community spillover effect would not decrease the total effect by much (-0.10 SDs, 95% CI: -0.8, 0.27).
5. What is the cost of delivering $1,000 worth of cash transfers?
We define cost to be the average cost the organization incurs when deploying an intervention. This is calculated by dividing the total expenses an organization incurred delivering an intervention by the number of interventions they delivered.
We extracted cost data from 29 cash transfers, 16 were delivered by NGOs, 10 by governments, and 3 that were unique to the academic studies they took place in. Most of these figures come from CTs outside of our sample as only four studies in our sample included information on operational costs. Since the cost of a cash transfer is contingent on the value of the cash that’s transferred, we standardized organizational expenses as “share of the transfer size”.
For monthly CTs we estimate that it costs a total of $1.27 to send a dollar. This additional cost beyond the transfer size ranges from 4% to 84% in our sample of monthly CTs. To put it another way, it costs between $1.04 and $1.84 to send a dollar. A histogram representing the distribution of operational costs can be viewed in Figure 6.
Figure 6: CT total costs as share of transfer size.

To retrieve the non-transfer cost of delivering a lump-sum CT we used cost data from GiveDirectly. GiveDirectly provides financial reports going back to 2012, the year it began operations. Its costs remain very consistent over time and scale as can be seen in Figure 7.
Figure 7: GiveDirectly average total cost per $1,000 transfer from 2012 to 2019

Note: This data was drawn from GiveDirectly’s public financial statements.
We estimate that the non-transfer cost of GiveDirectly CTs is lower than for monthly CTs (18.5% versus 27.73%). This isn’t surprising for a few reasons. First, GiveDirectly uses mobile banking. Many government and NGO monthly CTs do not. Second, monthly CTs by definition require multiple transactions which will lead to transaction fees constituting a larger share of the cost.
Table 3: Average non-transfer cost as share of transfer size
| Type of CT | Average cost as % of transfer size | SD of cost | Source |
| Monthly CTs | 27.73% | 0.196 | 29 CTs |
| GiveDirectly (lump-sum) CTs | 18.52% | 0.134 | 8 years of data |
6. Cost-effectiveness of $1,000 spent on cash transfers
6.1 Cost-effectiveness of existing interventions
Now that we’ve calculated the total effect and total cost of a cash transfer, we can put it into our standard units of how many SDs of well-being that can be bought with $1,000. This is simply the effect divided by the cost (which gives the benefit per dollar) multiplied by $1,000.29 We multiply by $1000 because we’ve found this produces easily readable units. We present the estimated cost-effectiveness of CTs in Table 4, alongside the per-person effects and per-transfer costs.
To get the estimate and its confidence intervals we ran Monte Carlo simulations in R where we assumed each parameter was independent of one another30 This includes independence between operational costs and CT effectiveness, which is plausibly related. To elaborate on the calculation, we present the R code, edited to be more legible. The following variables have simulated normal distributions: Total_effect = integral(intercept + size_effect + decay_rate*t), 0, duration)) ; cost = (1000 * (1 + cost_as_percent_of_transfer)). Then I calculate cost-effectiveness = totalEffect / cost. While this is the biased estimator, it only underestimates the unbiased estimate of the ratio (mean(totalEffect) / mean(cost)), by 0.7%. and drawn from a normal distribution. For the effects parameters we assumed that the mean was equivalent to the point estimate of the coefficient and the standard deviation would be equivalent to the standard error of the estimated coefficient. For the distribution of the cost, we assumed it took the mean and the SD of the cost data. This cost-effectiveness analysis is for the transfer values we expect to be used in CTs, so we think it worth considering: is $1,000 the most cost-effective amount to send in a lump-sum? We discuss some reasons for thinking that a smaller value could be more cost-effective in Appendix D.
Table 4: Estimated cost-effectiveness of lump-sum CTs and monthly CTs
| Cost to deliver $1,000 in CTs | Effect in SDs of wellbeing per $1,000 in CTs | SDs in wellbeing per $1,000 spent on CTs | |
| Lump-sum CTs | $1,185.16 ($1,098, $1,261) |
1.09 (0.329, 2.08) |
0.916 (0.278, 1.77) |
| Monthly CTs | $1,277.29 ($1,109, $1,440) |
0.50 (0.216, 0.920) |
0.396 (0.165, 0.754) |
Note: Below the estimate is its 95% confidence interval. The CIs were calculated by inputting the regression and cost results into a Monte Carlo simulation.
6.2 Is our analysis sensitive to the parameters we assume a value for but do not directly estimate?
Recall that there are two values in our CEA we explicitly assume and do not directly estimate. The first is the value of a monthly CT, which we let vary around the average quantity, between $10 and $30 dollars. Recall also that we fix the total value of monthly CTs at $1000. The second is the post transfer decay rate for monthly CTs, which we assume decays at the rate of lump-sum CTs. We estimate this value using the coefficient and its standard error given in Table 1, model (1).
The final cost-effectiveness of monthly CTs does not depend on the value of the CT for monthly CTs and the post transfer decay rate explains less than one percent of the variation in our results (R2 = 0.04% , 0.8%).
Since the sensitivity of our results to the other parameters is a function of their estimated variance and point estimates (given in Tables 1 & 2), we leave their discussion to Appendix C. There we also elaborate on our method for performing the sensitivity analysis.
6.3 Comparison of cash transfers to other interventions
Since we treat cash transfers as our benchmark intervention we make no detailed comparison to other interventions in this report. However, we do compare other interventions to CTs at the end of our other intervention reports. For example, you can view the comparison between GiveDirectly, monthly CTs, and delivered psychotherapy here.
The results of both of these comparisons are summarized in Figure 8 below. In this figure we display the uncertainty around our estimates of the average total effects and the average total costs. Each point is a single run of the simulation for the intervention. Lines with a steeper slope reflect a higher cost-effectiveness in terms of depression or distress reduction. The bold lines reflect the interventions cost-effectiveness and the grey lines are for reference. Our estimates for psychotherapy in general and psychotherapy delivered by StrongMinds in particular are more uncertain than CTs, but we estimate that they are more cost effective at improving affective mental health (we have little evidence of psychotherapy’s impact on SWB).
Figure 8: Cost-effectiveness of cash transfers compared to psychotherapy

Note: Each point is an estimate given by a single run of a Monte Carlo simulation. Lines with a steeper slope reflect a higher cost-effectiveness in terms of depression or distress reduction.
7. Discussion
We’ve excluded the spillover effects of CTs from our main analysis. We do this because household spillovers seem important, but highly uncertain. Importantly household spillover effects in terms of SWB or MHa information are sparse or missing entirely for other interventions we’ve considered. This means our comparison would be heavily influenced by a speculative parameter. This seems like reason enough to defer including spillovers until we have reasonable estimates not only for CTs but across interventions. We also think that the possibility that CTs extend the life of the recipients’ children is worth investigating.
At present we do not understand the mechanisms through which CTs improve the lives of their recipients. This limits the generalizability of this analysis to estimate the effects of income gains through other means.
For instance, we have little evidence regarding how the benefit of a CT depends on relative versus absolute gains. By relative we mean relative to peers versus an absolute improvement in material circumstances or an improvement relative to previous conditions. In other words, is the benefit due to recipients making beneficial comparisons to those who didn’t receive a CT or is it because of absolute change in the recipients living standards as a result of higher consumption? If the channel for CTs to improve SWB and MHa primarily runs through social comparison, then that would suggest that the effects would be smaller for an intervention that increases everyone’s income in an area.
8. Conclusion
In this analysis, we calculated the cost-effectiveness of GiveDirectly or a government transferring $1,000 to a recipient in an LMIC using SWB and MHa. We find that GiveDirectly CTs appear around three times (~2.7x) as cost-effective than government CTs. This is almost entirely (94%) because we estimate lump CTs to be more effective. The rest of the difference is due to GiveDirectly having lower operating costs. This cost-effectiveness will act as a benchmark to compare other interventions to.
Further research questions related to cash transfers
Through the course of this project, we arrived at some research questions related to cash transfers we did not have the time to answer. In Appendix F we rank them in order of perceived importance, state the question and explain how we would answer it if we had time.
Appendix A: Other models to explain the impact of cash transfers on SWB
Aside from a simple linear model, we also considered 1) a linear model without an intercept, models that assumed 2) a quadratic or 3) logarithmic relationship between SWB-$value and 4) a model that assumed that the benefits decay exponentially.
We chose to use a linear model that includes an intercept because it was the best fit for the data, and when the sample size is small we prefer a simpler model. However, an intercept, if large, has odd implications since it implies there would be a positive effect for giving someone a trivially small amount of money. We also think it is plausible that the SWB-$value is non-linear or that the effect decays exponentially through time, which is the best fit for the data in the case for psychotherapy. There are issues with using each of these models.
1) Forcing a linear regression to go through the intercept will bias its coefficients. For example, when we specify a no-intercept model, the model for monthly CTs flips its sign. The interpretation changes from estimating that the effects decay through time to growing through time while the transfers are ongoing. We still assume that the effects will decay once the transfers end, so the effects are not infinite. If we used a no-intercept model it would estimate the effects of CTs were 12% larger than the linear model (56% larger for lump-sum CTs and 33% lower for monthly CTs). See model 8 in Table A.5 and model 7 in Table A.6
2) We consider a model with a quadratic term for $value. An additional reason why we were hesitant to use this model, beyond not fitting the data as well as the linear model, was parsimony. We are concerned that fitting a more flexible model will overfit on the data when we would like to make more general predictions when possible. If we do implement a quadratic model, we find that it predicts a negative (but n.s.) quadratic term (implying a concave relationship) for lump-sum CTs and a positive (but n.s.) quadratic term (implying a convex relationship) for monthly CTs. The estimated total effects are lower in both cases (0.85 for lump CTs and 0.38 SD-years for monthly CTs). See model 11 Table A.5 and model 10 Table A.6
3) We also consider a model with $value log-transformed. This is the conventional relationship assumed between money and wellbeing in economics. In a y = β*log(x) model, the β coefficients can, for small changes in x, be interpreted as “percent change in x has an expected effect of β on y”. We can predict what the effect of a $1000 CT is using this model, i.e., y = β*log(1000). A model with a log($value) predicts substantially smaller effects than the linear model (0.63 for lump-CTs and 0.12 SD-years for monthly CTs). See model 9 in Table A.5 and model 8 in Table A.6
4) An issue with specifying that the effects of CTs decay exponentially is that we cannot do this while keeping $value as a variable that has, in our view, a sensible interpretation. Stipulating that the effects decay exponentially also means we must assume that the wellbeing-money relationship is a convex relationship (i.e. increasing at an increasing rate). This relationship is the opposite of the concave relationship commonly assumed between money and happiness.
While it may appear that if we log transform $value, this could return the $value to a linear relationship with wellbeing. This is not the case, because:
![]() .
.
This means that the log transformation does not return the desired concave or linear relationship. The relationship remains convex. However, if we take the double-log of CT-value, the value term becomes, ![]() , which is concave.
, which is concave.
If we use the exponential model exp(SWB) ~ $value + time it returns what appear to be implausibly high estimates of the initial effect (~3 SDs) and of the total effect of CTs (between 47-64 SD-years) because of the exponential relationship between CT $value and SWB.
However, if we took the double log of CT-value in an exponential model it would return more plausible values for the initial effects (0.2 – 0.55 SDs). But the total effects of CTs would still be much higher than the linear model predicts (5x larger for lump-sum CTs and 7x larger for monthly CTs). The effects are much larger than what is predicted by the linear model because the decay rate is estimated to be very low (9% a year for lum-CTs and 2% a year for monthly-CTs). See models 7 and 10 in Tables A.5 and models 6 and 9 Tables A.6 for the results of the exponential models.
Appendix B: Monthly CTs total effect example calculation
In this appendix, we calculate the wellbeing spending $1,000 on a monthly-CT provides its direct recipient. In this case, we assume they will receive the average monthly value of around $20. So the post-intervention effect ![]() = intercept + (0.613* $value in thousands) = 0.086 + (0.613 * ( 2.1 * (20 /1000))) = 0.11 SDs, which is less than the effect of 0.24 SDS a $1000 lump CT would have. While someone is still receiving transfers the effect will decay at a rate of -0.014 SDs per year. So we next need to find out what’s the effect when the transfer ends.
= intercept + (0.613* $value in thousands) = 0.086 + (0.613 * ( 2.1 * (20 /1000))) = 0.11 SDs, which is less than the effect of 0.24 SDS a $1000 lump CT would have. While someone is still receiving transfers the effect will decay at a rate of -0.014 SDs per year. So we next need to find out what’s the effect when the transfer ends.
One thousand dollars will finance a $20 CT for 50 months or 4.2 years of transfers. So the effect will be (4.2 * -0.014) + 0.11 = 0.051 SDs. At what rate will the effect decay after the transfers end? As we discussed we think it’s reasonable to assume that after the transfers end the effects will decay at the same rate as lump-sum transfers, -0.028. Which is exactly twice as fast. At that rate, the recipient would only receive benefits for a further | 0.051 / -0.028| = 1.82 years.
Recall that we assume the decay rate because we do not directly observe many CTs that follow-up with their recipients after monthly transfers have ended.
To calculate the total benefit we can sum the benefit for the period when the transfers were ongoing with the period after the transfers ended. Sticking with geometry, we’d find the benefit of the first period by summing the area of a rectangle and triangle: (0.5 * 4.2 * (0.11 – 0.051)) + (4.2 * 0.051) = 0.34 SDs. The benefit gained in the second period is 0.5 * 1.82 * 0.051 = 0.05 SDs improvement in SWB and MHa. The total benefit of both periods is then 0.34 + 0.05 = 0.39 SDs. This value is less than the one provided in the simulation for similar reasons given in the main text.
Recall that an alternative way of expressing the total effect is to write it as d02/-2r (see the appendix of McGuire, Kaiser & Bach-Mortenson (2020) to see derivation). From that expression we can see that the difference between our simulation and calculation by hand is due to Jensen’s inequality. This is because E(![]() 2/-2r) >= E(
2/-2r) >= E(![]() )2/2E(-r).
)2/2E(-r).
Appendix C: Sensitivity analysis
Which parameters are the final cost-effectiveness estimates most sensitive to? To answer this question we use our simulated dataset of 5,000 linear models to explain the relationship between our model’s inputs and results. Specifically, we treat cost-effectiveness as the dependent variable and the input parameters as explanatory variables. To capture the sensitivity of an input on the results we add each variable in isolation and record its ![]() . We assume a higher
. We assume a higher ![]() for a parameter corresponds to a greater influence of the parameter on the estimated cost-effectiveness. The results of our sensitivity analysis are presented below in Table 3.
for a parameter corresponds to a greater influence of the parameter on the estimated cost-effectiveness. The results of our sensitivity analysis are presented below in Table 3.
The cost-effectiveness of GiveDirectly CTs is about equally sensitive to the intercept and the effect a particular value of a lump-sum CT has on SWB and MHa. The cost-effectiveness of GiveDirectly UCTs are next most sensitive to estimated decay effect and least sensitive to the operating cost. Monthly UCTs are most sensitive to the intercept, then the decay effect. The cost-effectiveness of monthly UCTs is relatively less sensitive to the $value-SWB relationship than GiveDirectly lump-sum CTs.
Table C1: R2 of each simulated parameter in explaining the cost-effectiveness
| intercept | $value effect | decay effect | cost | |
| GiveDirectly | 35.7% | 36.8% | 18.3% | 3.0% |
| Monthly UCTs | 42.2% | 5.5% | 33% | 4.2% |
Appendix D: What is the most cost-effective transfer value?
GiveDirectly sends $1,000 CTs. We have some reasons to think that sending a smaller amount would be more cost-effective, but we’re unsure what transfer value is the most cost-effective. First, our across-study regression results suggest a mild relationship between the value of the CT and its effect. The presence of the significant and large intercept present in our regression results implies that smaller CTs within the range of lump-CTs studied in our sample ($97 to $1000) would be more cost-effective.
As we remarked previously, we don’t think our model seriously implies that a $0.01 CT is the most cost-effective because we observed no lump-CTs that small. While Ohrnberger et al, (2020) and Powell-Jackson et al, (2016) provided lump-CTs of $19 and $13, they were also amongst the studies that McGuire, Kaiser and Bach-Mortenson (2020) found as having the highest risk of bias, so we do not think they contribute much information to estimating the cost-effectiveness of small cash transfers.
When we regress the cost-effectiveness of lump-CTs31 We calculated the effectiveness by multiplying the effect times its duration, which assumes similar decay rates across CTs. We estimated the cost as the transfer value + the non-transfer cost. We calculated the non-transfer cost following Haushofer & Shapiro (2016) which described the non-transfer cost of a GiveDirectly CT as a fixed fee of $50 and a variable cost of 6.3% (p. 1979) . studied in RCTs against the transfer value, assuming a quadratic relationship, it does not return a significant relationship. We plot the relationship in Figure 9.
While the between study evidence is inconclusive, the within-study comparisons indicate that smaller transfer values are more cost-effective. Variation in transfer size cost-effectiveness captured by two studies of GiveDirectly CTs: McIntosh & Zeitlin (2020), Haushofer & Shapiro (2016). In Haushofer & Shapiro (2016) they distributed two CTs of $300 and $1000. In McIntosh & Zeitlin they tested four CTs $317.16, $410.65, $502.96 and $750.30. The larger CTs lead to larger effects in both studies, but not enough to offset their increased costliness.
Figure 9: Cost-effectiveness of lump-CTs

Appendix E: Robustness checks
Table E.1: Robustness checks for lump CTs (part 1 of 3)
| Coefficient | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 |
| intercept | 0.118 | 0.123 | 0.190 | 0.105 | 0.125 |
| 0.044 | 0.060 | 0.060 | 0.042 | 0.048 | |
| lump $value PPP in thousands | 0.058 | 0.058 | 0.030 | 0.056 | 0.067 |
| 0.045 | 0.053 | 0.044 | 0.043 | 0.053 | |
| years since transfer | -0.026 | -0.029 | -0.028 | -0.025 | -0.029 |
| 0.013 | 0.006 | 0.006 | 0.006 | 0.006 | |
| sample is less poor | -0.005 | ||||
| 0.068 | |||||
| baseline HH income in thousands | -0.199 | ||||
| 0.130 | |||||
| measure is SWB | 0.025 | ||||
| 0.015 | |||||
| by GiveDirectly | -0.016 | ||||
| 0.063 | |||||
| initial effect | 0.240 | 0.245 | 0.253 | 0.248 | 0.266 |
| duration | 9.145 | 8.591 | 8.882 | 9.896 | 9.248 |
| total effect | 1.099 | 1.054 | 1.121 | 1.228 | 1.231 |
Table E.2: Robustness checks for stream CTs (part 1 of 3)
| Model 1 | Model 2 | Model 3 | Model 4 | |
| intercept | 0.087 | 0.090 | 0.081 | 0.099 |
| 0.025 | 0.027 | 0.024 | 0.025 | |
| Monthly PPP $value | 0.001 | 0.001 | 0.001 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | |
| years since transfers began | -0.014 | -0.014 | -0.016 | -0.012 |
| 0.005 | 0.005 | 0.005 | 0.006 | |
| baseline HH income | -0.025 | |||
| 0.026 | ||||
| sample is less poor | -0.029 | |||
| 0.022 | ||||
| isSWB estimate | 0.029 | |||
| 0.012 | ||||
| CTisCCT estimate | -0.041 | |||
| 0.021 | ||||
| initial effect | 0.117 | 0.120 | 0.133 | 0.120 |
| monthly payment size | 20.000 | 20.000 | 20.000 | 20.000 |
| years of transfers | 4.167 | 4.167 | 4.167 | 4.167 |
| effect at end of CT | 0.061 | 0.064 | 0.067 | 0.072 |
| effect in transfer period | 0.371 | 0.384 | 0.418 | 0.400 |
| decay after transfer ends | -0.029 | -0.028 | -0.025 | -0.029 |
| effect post transfer | 0.064 | 0.071 | 0.090 | 0.089 |
| total effect | 0.435 | 0.455 | 0.508 | 0.489 |
Table E.3: Robustness checks for lump & stream CTs (part 2 of 3 for both)
| Model 6 | Model 5 | ||||
| intercept | 0.100 | intercept | 0.070 | ||
| 0.031 | 0.021 | ||||
| lump $value PPP | 0.006 | CT_PPP | 0.001 | ||
| 0.032 | 0.000 | ||||
| years since transfer | -0.013 | yearsSince | -0.015 | ||
| 0.006 | 0.005 | ||||
| Happiness | -0.012 | Happiness | 0.066 | ||
| 0.019 | 0.038 | ||||
| Life Satisfaction | 0.045 | Life Satisfaction | 0.029 | ||
| 0.024 | 0.016 | ||||
| Other MH measure | 0.051 | ||||
| 0.033 | |||||
| Other SWB measure | 0.143 | OtherSWB | 0.064 | ||
| 0.041 | 0.015 | ||||
| Both SWB and MH index | 0.059 | ||||
| 0.028 | |||||
| Depression | HP | LS | Dep | HP | LS |
| 0.489 | 0.389 | 0.964 | 0.224 | 0.770 | 0.425 |
Table E.4: Robustness checks for lump-CTs (part 3 of 3 )
| Model 7 | Model 8 | Model 9 | Model 10 | Model 11 | |
| exp | 0-intercept | log-val | log-loglog | quadratic-val | |
| intercept | 1.126 | 0.181 | 1.357 | 0.103 | |
| 0.049 | 0.032 | 0.133 | 0.062 | ||
| lump $value PPP | 0.086 | 0.157 | 0.113 | ||
| 0.051 | 0.036 | 0.149 | |||
| years since transfer | -0.034 | -0.027 | -0.028 | -0.090 | -0.029 |
| 0.006 | 0.006 | 0.006 | 0.049 | 0.006 | |
| log(lump $value PPP) | 0.025 | ||||
| 0.023 | |||||
| log(log(lump $value PPP)) | 0.049 | ||||
| 0.064 | |||||
| (lump $value PPP)^2 | -0.028 | ||||
| 0.073 | |||||
| initial effect | 0.330 | 0.189 | 0.218 | ||
| duration | 12.072 | 6.686 | 7.646 | ||
| total effect | 1.993 | 0.631 | 0.835 |
Table E.5: Robustness checks for monthly-CTs (part 3 of 3)
| Model 6 | Model 7 | Model 8 | Model 9 | Model 10 | |
| exp | 0-intercept | log-value | log-loglog | quadratic | |
| intercept | 1.091 | 0.022 | 0.014 | 0.093 | |
| 0.025 | 0.062 | 0.072 | 0.034 | ||
| Monthly PPP $value | 0.001 | 0.0014 | 0.000 | ||
| 0.000 | 0.0002 | 0.001 | |||
| years since transfers began | -0.015 | 0.0003 | -0.014 | -0.014 | -0.014 |
| 0.005 | 0.0065 | 0.005 | 0.005 | 0.005 | |
| log(Monthly PPP $value) | 0.026 | ||||
| 0.015 | |||||
| log(log(Monthly PPP $value)) | 0.082 | ||||
| 0.053 | |||||
| (Monthly PPP $value)^2 | 0.000 | ||||
| 0.000 | |||||
| initial effect | 0.058 | 0.056 | 0.000 | 0.110 | |
| monthly payment size | 20.000 | 20.000 | 20.000 | 20.000 | 20.000 |
| years of transfers | 4.167 | 4.167 | 4.167 | 4.167 | 4.167 |
| effect at end of CT | 0.064 | 0.000 | 0.053 | ||
| effect in transfer period | 0.254 | 0.116 | 0.339 | ||
| decay after transfer ends | -0.027 | 0.000 | -0.029 | ||
| effect post transfer | 0.075 | 0.000 | 0.049 | ||
| total effect | 0.139 | 0.116 | 0.387 |
Appendix F: Research Questions
How much does the recipient household benefit from a CT relative to the main recipient? What does that household spillover depend on? This is the most important further question to answer. Comparing interventions based on the total household effects could change our conclusions.
As we mentioned in footnote 25, there are more studies we could use to extract household spillover effects. If we had more time we would try and estimate the household spillover effects in those studies. It seems plausible that household spillover effects will also vary depending on the size of the CT. For instance, people could share more after receiving more generous CTs. Additionally, the characteristics of the recipient may matter. For example, women and the elderly may share more with the household.
Many studies might have captured the data necessary to estimate household spillover effects but did not think to use it. A next step would be to email researchers and ask them for data or any unreported results related to household spillovers. Does a study record more individuals than households? If so, that may identify studies that likely capture household spillovers.
What mechanisms drive CTs benefit to SWB and MHa? How much of the benefit is due to decreases in relative versus absolute poverty? Similarly, do income changes need to be above a certain threshold to have an impact? That is, do tiny changes in income matter? Presumably, noticing that your income has increased plays a part in its benefit. Some positive income changes may fail to register as a noticeable difference.
Do CTs decrease mortality in the recipient’s household? Does this depend on whether the CT is conditional? This question merits a separate literature review. If a review finds large effects, it would merit a revision and expansion of this CEA. To answer this question we would synthesize the literature. Particularly, we see if the effect depends on the conditionality and size of the cash transfer. A related question is how much do adding conditions to CTs cost? This would allow a cost (and cost-effectiveness) comparison between conditional and unconditional CTs.
How would our results change if we performed an individual level meta-analysis? To answer this, we would pool data from existing studies with open access data. These studies are Haushofer & Shapiro (2016), Ohrnberger et al., (2020), Paxson et al., (2010), Macours et al., (2012), Molotsky & Handa (2021) and Blattman et al., (2020). Then we would request data from other authors.
Here are some other less urgent questions. Does receiving a cellphone and m-Pesa enrollment have an effect on SWB? What percent of payments do recipients typically receive from government CTs? Is receipt of government CTs associated with an uptake in other government services?
