Happiness for the whole family
- Happiness for the whole family
- Executive Summary
- Outline
- 1. Introduction
- 2. Data
- 3. Methods
- 4. Results
- 5. Robustness checks
- 6. Limitations and future steps
- 7. Conclusion
- Appendix A: Description of spillover studies
- Appendix B: Estimating the household size
- Appendix C: Robustness checks
November 2023: Update to our analysis
We have made a substantial update to our psychotherapy report. This 90+ page report details new methods as well as an updated cost-effectiveness analysis of StrongMinds and a novel cost-effectiveness analysis of Friendship Bench. We now estimate StrongMinds to produce 30 WELLBYs per $1,000 donated (or 3.7 times more than GiveDirectly cash transfers).
See our changelog for previous updates.
Executive Summary
We update our earlier cost-effectiveness comparison of psychotherapy and cash transfers (both implemented in low-income countries) by including an estimate of the total household effects. Our previous analysis only considered the effects on recipients. For cash transfers, we estimate from eight studies that each household member experiences 86% (95% CI: 43%, 154%) of the benefits experienced by the recipient. For psychotherapy, we estimate from three studies the spillover ratio to be 53% (95% CI: 11%, 108%). After including the household spillover effects, we estimate that psychotherapy is 9 times (95% CI: 2, 100) more cost-effective than cash transfers (before it was 12 times). The charity StrongMinds is estimated to be 9 times (95% CI: 1, 90) more cost-effective than the charity GiveDirectly (before it was also 12 times). Our household analysis is based on a small number of studies, eight for cash transfers and three for psychotherapy. We conducted several robustness checks. We found psychotherapy (and StrongMinds) to be at least five times more cost-effective than cash transfers (and GiveDirectly) in all cases. The lack of data on household effects seems like a gap in the literature that should be addressed by further research. We show that including household spillovers can change the relative cost-effectiveness of two interventions, which demonstrates the need to account for the impact of interventions beyond the direct recipient.
Outline
- In Section 1 we explain why we wrote this report, flag its limitations, and motivate the case for household spillovers existing in interventions that improve wellbeing.
- In Section 2 we describe the data we use for estimating the household spillovers for cash transfers and psychotherapy (see also Appendix A).
- In Section 3 we walk through the methods we use to calculate household spillovers.
- In Section 4 we present and discuss the results of our analysis of household spillovers and how they update our cost-effectiveness analysis and comparison of interventions.
- In Section 5 we summarise the results of our robustness checks (see also Appendix C).
- In Section 6 we expand on the limitations of our research, and note the most promising paths for future research on the topic of household spillovers.
- In Section 7 we conclude by summarising our results.
1. Introduction
1.1 Why are we doing this analysis?
In 2021, we analysed the cost-effectiveness of cash transfers, psychotherapy, and the charities GiveDirectly and StrongMinds; all of these occurred in low-income countries. This work resulted in a cost-effectiveness comparison of psychotherapy and cash transfers as well as between StrongMinds and GiveDirectly. We found that psychotherapy was about 12 times more cost-effective than monthly cash transfers.1Note that, just like in our previous analyses, when we evaluate ‘GiveDirectly’ we mean ‘GiveDirectly and lump-sum cash transfers’ (a specific subset of cash transfers), and when we evaluate ‘cash transfers’ we mean ‘monthly cash transfers’ (the most common type of cash transfers). Our previous analyses showed that GiveDirectly and lump sum cash transfers were more cost-effective than monthly cash transfers. We also found that StrongMinds (which provides group psychotherapy) was about 12 times more cost-effective than GiveDirectly (which provides lump-sum cash transfers).
In the first version of our analysis, we only estimated the effects on the direct beneficiaries of those interventions. However, an intervention can also have ‘spillover’ benefits (also known as the ‘knock-on’ or ‘second-order’ impact of the intervention) on people besides the recipient. There can be effects on the recipient’s household (household spillovers) and/or their community (community spillovers). Other members of the household (e.g. partner, parents, and children) have close contact with the recipient and, thereby, may be substantially affected. However, we did not include household spillovers in our previous analysis because of the considerable uncertainty about the relative magnitude of spillovers across interventions and the dearth of evidence with which to estimate the household spillover effects. Our analysis was critiqued (on Twitter and the Effective Altruism forum) for omitting household spillovers; the concern being that this was a non-trivial omission which could substantially reduce the relative cost-effectiveness advantage of psychotherapy.
As a result, we conducted an extensive search for data on the household spillovers of cash transfers and psychotherapy. We found a small number of studies with information about the effects on non-recipient household members: eight for cash transfers (studying six unique cash transfers) and three for psychotherapy (studying three unique psychotherapy interventions). This limited evidence lends sizable uncertainty to our analysis. Nevertheless, this is the most reasonably rigorous analysis we can do until more data becomes available. It allows us to estimate spillover ratios for psychotherapy and for cash transfers, estimate the benefit of each intervention on the whole household, and, therefore, compare the cost-effectiveness of the interventions. Psychotherapy’s cost-effectiveness advantage over cash transfers does decrease when accounting for household spillovers, but only by a little.
Additionally, the lack of data on household spillovers means we can only provide limited answers to questions that often accompany discussions of household spillovers: Does a non-recipient household member receive more spillover benefits if they are in a small or large household? Does the relationship between the recipient and household member (e.g. parent to child or partner to partner) affect spillover benefits? Our evidence finds a small, non-significant relationship for both questions (but these analyses are likely underpowered). Therefore, we assume the household spillover effect will be the same for any non-recipient household member. We discuss this more in Section 3.3.
Both in our previous analysis and in this one, we omit community spillovers between households because our previous analysis suggested that, both for psychotherapy and cash transfers, the effects were similarly close to zero and were unlikely to affect this comparison. See Section 4.2 of our cash transfers report and Section 4.3 of our psychotherapy report for more details.
It is important to understand that our analysis does not estimate whether it is better to provide psychotherapy or a cash transfer to a randomly selected resident of a low-income country. Psychotherapy is only provided to people with depression, whereas cash transfers go to the poor in general. Hence, while GiveDirectly’s beneficiaries are very poor (and some may be depressed), StrongMinds beneficiaries are very poor and all of them are depressed. Presumably, these interventions would have different costs and effects if they targeted different populations.
1.2 Possible spillover mechanisms
This section motivates why cash transfers and psychotherapy could have sizable spillover effects. Discussion of the possible causal mechanisms is important because intuitions about spillover effects seem to differ between academic disciplines. Economically-trained people we have spoken to think it is obvious that cash transfers would have larger household spillovers, whereas psychologically-trained individuals assume that psychotherapy will have similar or larger household spillovers than cash transfers.
We think household spillovers can occur in at least two ways: emotional contagion and economic contributions. This is not an exhaustive or mutually exclusive list and there may be bi-directional interaction effects. Our goal is to illustrate to the reader that there are mechanisms by which both psychotherapy and cash transfers might plausibly produce household spillovers rather than provide a neat account of the nature and relative strengths of these dynamics. We illustrate these causal mechanisms in Figure 1 below then describe each mechanism in more detail. The lines connecting the nodes should be read as possible mechanisms. Not every intervention will work through every illustrated path.
Figure 1: Possible causal mechanisms for spillover effects
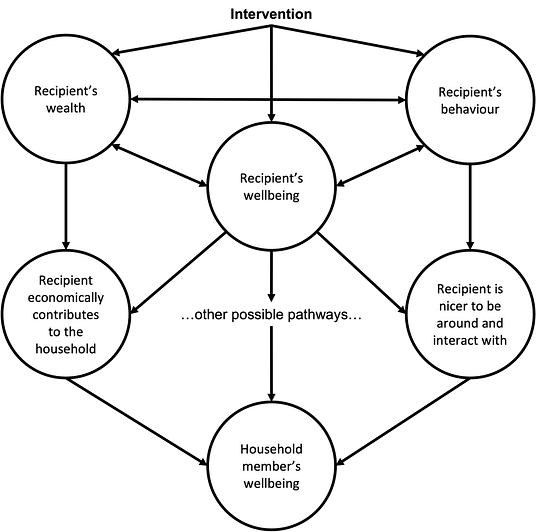
1.2.1 Emotional contagion
Emotional contagion refers to how good or bad moods are transmissible. It is pleasant to be around someone joyful and difficult to be near someone who is suffering. A longitudinal network analysis of more than 5,000 participants from 1971 to 2003 (the Framingham Heart Study) found that the likelihood of becoming happier increases when nearby connections become happier (Fowler & Christakis, 2008). Additionally, longitudinal panel studies show that levels of life satisfaction correlate across time between parents and their children (Chi et al., 2019; Headey et al., 2014). For example, in a German panel study, the correlations between parents’ and children’s five-year moving averages of life satisfaction varied between 0.31 and 0.42 (Headey et al., 2014).
Similarly, the effects of low mental health are ‘contagious’ within a household. People’s mental health decreases if their close connections have lower mental health (Das et al., 2008; Rosenquist et al., 2011). This contagion applies to partners (McNamee et al., 2021) and parent-child relationships (Goodman, 2020; Goodman et al., 2011; Johnston et al., 2013; Powdthavee & Vignoles 2008; Olfson et al., 2003; Walker et al., 2020; Zheng et al., 2021). An analysis of household surveys in low- and middle-income countries found that “a one standard deviation change in the mental health of household members is associated with a 0.22–0.59 standard deviation change in own mental health” (Das et al., 2008, p. 43). Looking at the Framingham Heart Study, Rosenquist et al. (2011) found that participants who had a close connection with a person with depression were 93% more likely to be depressed. Whilst we do not draw causal conclusions from these correlational findings, they support the idea of emotional contagion.
Emotional contagion could explain part of the spillovers for both psychotherapy and cash transfers. If someone receives an intervention that improves their wellbeing, their household will likely notice. The recipient may express more positive affect and less negative affect than before, which, in turn, will improve the wellbeing of their household members.
Similarly, an intervention, either through increased wellbeing or by behavioural change, may improve interpersonal interactions. Improving interactions is a plausible pathway for both types of interventions. Cash transfers have been found to reduce domestic violence (Baranov et al., 2021). Providing psychotherapy for perinatal depression may improve mother-child relationships (Cuijpers et al., 2015). This seems particularly pertinent for interpersonal group therapy (which StrongMinds provides) because it focuses on improving relationships to ameliorate depressive symptoms.
1.2.2 Economic contributions
Economic contributions refer to how an intervention can improve how well someone contributes to the material welfare of their household. This contribution could come from an economic transfer that is shared or from increased productivity caused by better health (mental or physical) or skills training.
The economic contribution pathway seems most relevant for explaining the household spillovers for cash transfers. Either because recipients share the cash with household members or purchase common goods that benefit the entire household. GiveDirectly recipients report spending most of their cash transfers on household common goods. In Kenya, they report spending 56% of their cash transfers on building improvements, 7.6% on livestock, and 4.8% on other household goods (GiveWell, 2016). It is unclear how this remaining amount is shared between household members.
Economic contributions may also explain part of the household spillovers for psychotherapy. Indeed, the relationship between poverty and mental health seems bidirectional: poverty causes low mental health, but low mental health also causes poverty (Ridley et al., 2020). The presence of mental health problems hinders education and skill acquisition (Johnston et al., 2013), lowers productivity (Mall et al., 2015), employment (Das et al., 2008), and adds health expenditures (Das et al., 2008; Lund al., 2019). Low mental health is also correlated with lower household income (Lund al., 2019).
Just as low mental health seems related to poverty, improving mental health corresponds to better economic outcomes. There is some evidence from panel data that accessing psychotherapy (Cozzi et al., 2018) or pharmacotherapy (Angelucci & Bennet, 2021) can increase individuals’ incomes. See also a meta-analysis by Lund et al. (2020) and a review by Lund et al. (2011). Analysing the British Household Panel Survey data, Cozzi et al. (2018) found that consulting a psychotherapist, controlling for the potential costs of therapy, predicted increases in income (12% for men and 8% for women). Therefore, if a household member receives psychotherapy, they might also become more productive and benefit the household economically. This relationship seems plausible because psychotherapy treats people who are depressed and may be unable to engage in economic activities without treatment.
We expected the emotional contagion benefit to non-recipient household members to be roughly equivalent between cash transfers and psychotherapy. Some types of psychotherapy (interpersonal) and cash transfers (conditional) explicitly target interpersonal interactions, but we were unsure which would benefit the household more. We also expected the economic contributions mechanism to be stronger for cash transfers than for psychotherapy. Therefore, we expected greater household spillover benefits for cash transfers than psychotherapy. Consequently, we anticipated a drop in the relative cost-effectiveness advantage of psychotherapy when we added the household benefit. Nevertheless, we still need to obtain data to estimate the spillover effects.
2. Data
We sought data from studies that measured the impact of an intervention on both recipients and members of the recipients’ households. None of the studies from which we obtain this data primarily investigate household spillovers. Rather, the studies provide the information as a secondary outcome and we use this to conduct a novel analysis. The data we selected had to fulfil the following criteria: (1) they provided either cash transfers or psychotherapy to individuals; (2) they measured participants’ self-reported changes in mental health or subjective wellbeing compared to a control group; (3) they also measured self-reported changes in mental health or subjective wellbeing of at least one household member compared to a control group;2Note that, for all included studies, only one non-recipient household member was surveyed. and (4) the household member must not have received the intervention.
Hence, we are looking for pairs of effect sizes. The first element is an effect on the direct recipient and the second is an effect on the non-recipient household member. When interventions conducted follow-ups to measure the intervention results over time (i.e., they ask participants to answer surveys again, at a later point), we collected the effect sizes at every follow-up available.
In total, for our main analysis, we obtain eight studies for cash transfers (studying six unique cash transfers) and three for psychotherapy. Whilst not a completely systematic search, we view this search as relatively exhaustive and do not think additional searching would yield additional evidence in the published literature.3A study by Desrosiers et al. (see their 2020 protocol) investigating the spillovers of mental health intervention in Sierra Leone might provide more data in the future. Preliminary results are not yet available. As such, we do not think a more rigorous analysis is feasible until more data are collected.
2.1 Cash transfers data
We obtained data for calculating the cash transfers spillover from our initial (individual-level) analysis. This analysis was the result of a systematic meta-analysis of 45 studies measuring the effect of cash transfers on subjective wellbeing and mental health in low- and middle-income countries (McGuire et al., 2022). Our search yielded household spillovers from six cash transfer interventions. These studies provided nine recipient-household member pairs of effect sizes and a total sample of 35,961 unique participants. In every study but Baird et al. (2013), the spillover effects of cash transfers to other household members are positive. We describe the studies in Appendix A.
Note that the data for non-recipient household members for the GiveDirectly program came from Haushofer et al. (2019), which is originally disaggregated across gender (cash transfers given to women vs. cash transfers given to men). Whilst this makes sense for their analysis, it does not for ours (none of our other results are disaggregated across gender), so we combined the effects.4Keeping the results disaggregated across gender leads to a higher cash transfers spillover ratio, and, thereby, a lower relative cost-effectiveness advantage for psychotherapy. See Section 5 and Appendix C2 for more details.
As with our individual level analysis for cash transfers, we included both conditional (2 interventions) and unconditional (4 interventions) cash transfers. Conditional cash transfers might change participants’ behaviours (in order to obtain the cash transfer) in specific ways that unconditional cash transfers would not. However, whichever the mechanism, they provide information relevant to estimating the cash transfer spillover. Removing them does not severely change the results.5Removing conditional cash transfers lowers the cash transfer spillover so psychotherapy’s cost-effectiveness advantage compared to cash transfers is slightly higher than in our current analysis (whilst psychotherapy remains 9 times more cost-effective than cash transfers, StrongMinds becomes 10 times more cost-effective than GiveDirectly).
2.2 Psychotherapy data
For psychotherapy, only one study from our initial analysis of 39 studies of psychotherapy (Baranov et al., 2020) included a measure of wellbeing for a household member, but this was a mother’s report about their child’s wellbeing instead of a self-report. We also found data from Mutamba et al. (2018), but did not include it in our previous analysis because they had not randomly allocated participants to the control and treatment groups. We include it for estimating the spillover ratio since we believe that a ratio of effects within a study will be less susceptible to bias stemming from non-randomization.6The reasoning is that random allocation will likely change the absolute magnitude of the recipient and non-recipient household effects, but not their relative magnitude since many biases will apply equally to both household members.
Because we found so few studies of household effects in low- and middle-income countries, we expanded our search to high-income countries. We also contacted academic experts (four for cash transfers, six for psychotherapy.7The ones that replied were Pim Cuijpers from Vrije Universiteit Amsterdam, Crick Lund from King’s College London, Vikram Patel from Harvard Medical School, and Victoria Baranov from the University of Melbourne.) We investigated studies mentioned in Cuijpers et al.’s (2015) meta-analysis on perinatal maternal depression and searched Google Scholar.8The topics we searched Google Scholar for included psychotherapy, mindfulness, or positive psychology interventions related to households, parents, children, or spouses/partners. Lastly, we systematically searched Cuijpers and colleagues’ unreleased database of 321 psychotherapy studies added since 2015 (the ones present before should have been covered by their 2015 meta-analysis). We believe this is the most exhaustive extant database.9This database was the latest but currently unreleased version of their psychotherapy database. The old version included all psychotherapy studies until 2019. The new version spans 2019 to 2021. Cuijpers and colleagues shared all the studies they planned to include, which we manually sorted through by title and abstract. First, we sorted through 321 studies to select studies that likely included household effects, leaving us with 44. Out of those, we read the papers to verify if they met our inclusion criterion, resulting in one additional study. This search yielded nine additional studies.
However, seven of the ten studies (the nine additional studies plus Mutamba et al.) use measures of children’s mental health or subjective wellbeing that are observer reports, assessments made by the children’s parents (or the researchers) instead of self-reports. Our belief is that we should ultimately care about individuals’ self-reports of their subjective wellbeing and mental health, rather than other people’s assumptions of how someone else’s life is on the inside. Critically, self-reports do not rely on other people’s guesses or inferences.10A meta-analysis found that observer reports only have a moderate (r = 0.41) correlation to self-reports of wellbeing (Schneider & Schimmack, 2009). It is unclear whether observers have a systematic bias when predicting others’ wellbeing, but affective forecasting errors suggest that it is likely.
Hence, for our main analysis, we only use effect sizes that involve self-reports. From our search, this leaves us with three studies (Kemp et al., 2009; Mutamba et al., 2018; Swartz et al., 2008), that provide us with five pairs of effect sizes and a total sample size of 410 unique participants. One of these studies (Mutamba et al., 2018) investigates psychotherapy in a low- and middle-income country, the rest are in high-income countries.
A limitation to the external validity of this evidence is that all of the samples were selected based on negative shocks happening to the children in the sample. In Kemp et al. (2009), children received EMDR for PTSD symptoms following an automobile accident. In Mutamba et al. (2018), caregivers of children with nodding syndrome received group interpersonal psychotherapy. In Swartz et al. (2008), depressed mothers of children with psychiatric illness received interpersonal psychotherapy. We are not sure if this would lead to an over or underestimate of the treatment effects, but it is potentially a further deviation from the type of household we are trying to predict the effects of psychotherapy for. Whilst recipients of programmes like StrongMinds might have children who have experienced negative shocks, we expect this is not the case for all of them.
We describe the studies in more detail in Appendix A.
3. Methods
3.1 General method for obtaining intervention effects
Readers not interested in the methodological details, or those familiar with the methods we employed in previous reports, can likely skip this section.
Ideally, we would calculate the household’s benefit in the same way we calculated the recipient’s benefit in our cash transfer and psychotherapy reports, and using the same studies. However, except for six cash transfer interventions, the data we used for our previous reports do not contain information about household members’ benefits.
Since we do not have household spillover data from the same contexts, we model household member benefits in terms of a spillover ratio S, estimated from the data presented in Section 2. The spillover ratio is the proportion of the recipient’s benefit that a non-recipient household member experiences. We measure the household spillover effect as the share of benefit the household member received compared to the recipient. We report the expected spillover effect as a point estimate and the range of uncertainty as confidence intervals around our estimates. We can then apply the estimated spillover ratio to the data from our previous reports to obtain the overall household benefits.11We assume the ratio of effects obtained from this different data context is more generalisable than the average effect we find on a non-recipient household member obtained from this different data context. See Section 5 and Appendix C6 for more details.
We use Monte Carlo simulations to model the uncertainty, as we did in our previous cost-effectiveness analyses. In a simulation, we run each calculation 10,000 times. In each run, every estimate is drawn from a normal distribution. We centre each distribution on the average and we estimate the variance from the spillover data. In the case of results obtained via a meta-analysis, the mean of the simulated distribution is set by the average effect size we estimate. Similarly, the standard deviation of the distribution is set to be the estimated standard error of the average effect. Using the simulation allows us to obtain 95% confidence intervals (the 2.5th percentile and 97.5th percentiles of the simulated distributions) for each parameter we estimate.12 In previous reports, we used the 5th and 95th percentiles because this is what Guesstimate provides. The 5th and 95th percentiles correspond to a 90% confidence interval, which we mistakenly reported as a 95% confidence interval. This introduces slight differences in the values reported within our previous reports but does not affect the relative magnitude between psychotherapy and cash transfers. Differences also arise from random variation in the Monte Carlo simulations. We also solely use R instead of Guesstimate to estimate the individual effects of psychotherapy. Our previous reports reported the mean of the simulated distribution instead of the point estimate calculated using arithmetics. This allows us to obtain measures of uncertainty for certain variables that we could not obtain otherwise. Notably, if we find the average effect and cost values using data, we can convert those summary statistics to variables with distributions using a Monte Carlo simulation. Then we can divide the simulated cost and effect to find the distribution, and thus 95% confidence intervals, of the cost-effectiveness ratio. The point is that, without using a simulation, we could not estimate the uncertainty in our results.13 This would require having the cost and effect information in each study, which would reduce our sample size and rely on taking the average ratio instead of the ratio of averages (which we discuss in Appendix C6).
As with our previous reports, we standardise the effect sizes using Cohen’s d (see Lakens, 2013, for an explanation). Cohen’s d is interpreted as standard deviation differences between the intervention and control group. When we report confidence intervals for d values (in our figures notably), these are calculated using mean ± 1.96 * standard error (instead of percentiles like the confidence intervals from our Monte Carlo simulations).
We use meta-analyses to obtain the average household spillover effects. Simply put, this is an average of study effects weighted by the precision of the study. The smaller a study’s standard error (a function of the standard deviation and sample size), the greater its precision. A meta-analysis has the benefit of allowing one to estimate the uncertainty that comes from error within a study and the differences between studies (called heterogeneity). Some studies measure the effect of interventions at multiple time points and include multiple wellbeing questionnaires. Hence, these effect sizes are likely correlated (i.e., dependent). If this correlation is not accounted for, then the standard way studies are meta-analysed would underestimate the error in the average effect. We solve this issue by explicitly specifying the relationship between the effect sizes using a multi-level meta-analysis (Harrer et al., 2021; Viechtbauer, 2010).
Our individual recipient analysis calculated the total benefit the recipient received, not just the initial benefit. An initial benefit is an effect (in Cohen’s d) when the intervention ends. In our previous analysis, the studies varied dramatically in the time of their follow-ups and multiple studies provided several follow-ups. This allowed us to model how the effect of an intervention changed over time. The total benefit of an intervention is the sum of the benefit, in standard deviation differences, a recipient accrues over time.
In our present analysis, we do not have enough data to reasonably analyse how household spillovers change over time. In a footnote, we discuss the results if we perform the underpowered analysis.14 The decay rate of non-recipient household effects are imprecisely estimated. The estimated (linear) decay rate for the benefit of non-recipients in cash transfers is -0.024 SDs per year (95% CI: -0.08, 0.03), which is steeper than it was for the recipient in the individual analysis (-0.014 SDs per year). For psychotherapy, the decay is estimated to be positive 0.3451 SDs per year (95% CI: -1.34, 2.24) while the effect linearly decayed steeply in the individual analysis at -0.104 SDs per year (95% CI: -0.197, -0.010). We think it is implausible that the effects would grow for the non-recipient while they decay for the recipient. If we took these values seriously, it would dramatically improve the favorability of psychotherapy. But we do not think these are sensible figures to use. Instead of trying to separately estimate the decay rate for benefit on the non-recipient household, we assume that the spillover benefits will decline similarly to the recipient’s benefits. This assumption is consistent with our model that spillover effects stem from the recipient effects. Beyond that, it is unclear how reasonable this assumption is.
Given the small set of interventions we found with household spillover effects (six for cash transfers, three for psychotherapy), we only estimate intervention (not charity) level spillovers. There are no studies of StrongMinds and only one randomised control trial of GiveDirectly which contain data which is directly relevant for our spillover analysis. In this case, our best guess for the spillover ratio for the charities is the general case we find for the intervention as a whole.
3.2 Obtaining the spillover ratio
We estimate the percentage of the effect a recipient’s household member receives relative to the direct recipient as the spillover ratio S:
![]()
The ratios might be different between cash transfers and psychotherapy. Hence, we are looking for the spillover ratio for cash transfers (and GiveDirectly), ![]() , and the spillover ratio for psychotherapy (and StrongMinds),
, and the spillover ratio for psychotherapy (and StrongMinds), ![]() .
.
We use a Ratio of Averages method to estimate the ratio.15 Note that there are other methods to aggregate ratios or determine the household benefits. Whilst the Ratio of Averages is the most appropriate, we present results from (and reasoning against) alternative methods in Section 5 and in Appendix C6. This method means we obtain the average of the recipient’s benefit and the average of the household member’s benefit in the psychotherapy and the cash transfer datasets. Then we take the ratio of these averages:
![]()
To obtain these average effects (on the direct recipient and the non-recipient household member), we use a meta-analysis, as previously mentioned. However, only a few studies we found include follow-up data (Baird et al., 2013; Mutamba et al., 2018; Swartz et al., 2008). Therefore, this is a ratio of effects found within a timepoint, not a ratio of the total benefits.
3.3 Household size and household benefits
Once we have estimated the spillover ratio, S, we need to include the household size to estimate the overall household benefit. We assume the effect on the direct recipient will have the same spillover (according to S) to every other member of the household.
3.3.1 Reasoning and modelling about the effect on the household
The recipient’s household size and their relationship to other household members could influence how much benefit spills over to each household member.
It seems plausible that in a small household you are more likely to perceive the emotional changes in the recipient and/or would receive more of the economic benefits than in a large household. For this reason we predict a negative relationship between the household size and the household member effect. It is also possible that you will benefit differently if the recipient is your parent (and you were a child) than if they are your spouse (and you were an adult).
For each intervention obtained for our spillover data, we collect information about the average household size of participants in that intervention. This information is missing for some psychotherapy interventions, in which case we imputed household sizes using the country’s average. We test whether changes in household sizes or differences in the recipient-household member relationship affected the non-recipient household member effect. We find no significant relationship in either case.16 For cash transfers, every increase in household size would change the non-recipient household member effect by 0.016 Cohen’s d, which is close to 0 and not significant, p = .640. For psychotherapy, every increase in household size would change the household member effect by -0.057 Cohen’s d, which is not significant, p = .329. If cash transfers benefit the household because the recipient shares the cash, then the household benefit should decline the more people the cash transfer is split between. However, we do not think one should interpret this underpowered analysis seriously. In our cash transfers spillover data the household member effect does not significantly change depending on whether they are a child or an adult, Cohen’s d = -0.001, p = .866 (six effect sizes, not counting the child-child relations from Baird et al., 2013). This is unsurprising considering our limited data.
3.3.2 Estimating household size
For StrongMinds’ and GiveDirectly’s household sizes, we use the average household size for the African countries in which these charities operate (weighted by their share of operations in these countries). We assume that, in general, psychotherapy and cash transfer interventions could be deployed in any area of Sub-Saharan Africa. Hence, for the overall intervention-level comparison, we assign the same household size to psychotherapy and cash transfers. See Appendix B for more details on how we estimate the household size.
We use the non-recipient household size, the household size minus the recipient of the intervention. For StrongMinds, we find a non-recipient household size of 4.85 (95% CI: 1.01, 8.94). For GiveDirectly, the non-recipient household size is 3.93 (95% CI: 0.5, 8.27).17 We use different household sizes for StrongMinds and GiveDirectly because they operate in different countries (and to varying extents in said countries). However, we also conduct a version of this analysis using the same household size for each intervention. This further reduces the cost-effectiveness advantage of StrongMinds relative to GiveDirectly to 8 times. See Section 5. We use the same non-recipient household size for psychotherapy and cash transfers of 3.80 (95% CI: 2.03, 5.56).
3.3.3 Calculating the household benefit
We assume the benefit is the same for every household member who is not the direct recipient (as discussed above in Section 3.3.1). We obtain the non-recipient household benefit with:
![]()
We then add the non-recipient household benefit to obtain the overall household benefit:
![]()
From which we obtain cost-effectiveness for every 1,000 US dollars spent:18 We used the same cost inputs as discussed in the previous reports, except we truncated the normal distributions (using the msm package; Jackson, 2011) for our Monte Carlo costs simulations. The truncation was to avoid costs being negative.
![]()
We then compare the cost-effectiveness between psychotherapy and cash transfers:
![]()
4. Results
We find that 86% (95% CI: 43%, 154%) of the benefits of cash transfers spill over to each household member. In other words, a household of four members, one recipient and three other household members, would experience a total benefit of 1 + 3*0.86 = 2.58 times that of the direct recipient alone. The spillover ratio is lower for psychotherapy, 53% (95% CI: 11%, 108%). Incorporating these household spillovers reduces the cost-effectiveness advantage of psychotherapy (and StrongMinds) relative to cash transfers (and GiveDirectly). We find that psychotherapy is 9 times (95% CI: 2, 100) more cost-effective than monthly cash transfers and that StrongMinds is 9 times (95% CI: 1, 90) more cost-effective than GiveDirectly.
4.1 Cash transfers results
The studies that include effects on a household member found a significant effect of cash transfers on the wellbeing of the direct recipient, average Cohen’s d = 0.114, (95% CI: 0.07, 0.16). This is the effect at an average follow-up of nearly two years (this is neither the initial effect nor the total effect, but the effect at the time of the average follow-up). We also found a significant effect of cash transfers on the wellbeing of the household member, average d = 0.098, (95% CI: 0.04, 0.15). Because of the small sample size of studies (eight in general, one for GiveDirectly), we assume that the spillover ratio for cash transfers, in general, is the same as GiveDirectly, in particular. After taking the ratio of these two figures we find that the non-recipient household member receives ![]() = 0.098/0.114 = 86% (95% CI: 43%, 154%) of the recipient’s benefit. Recall that we used a simulation to find the confidence intervals.
= 0.098/0.114 = 86% (95% CI: 43%, 154%) of the recipient’s benefit. Recall that we used a simulation to find the confidence intervals.
Below, in Figure 2, we show a forest plot of the recipient and household effects of receiving a cash transfer. On the left of the plot, we label the intervention-time point combination. Points represent the average treatment effect in standard deviation changes in subjective wellbeing. Their size grows with larger sample sizes. Whiskers represent the 95% confidence intervals. Dotted lines for whiskers represent an effect on a child, and full lines represent an effect on an adult (or the average estimate). The colour of the point and whisker is orange if it corresponds to the recipient and grey for the household member. To the right of the points, we numerically display the same information, the average and confidence interval. Below the interventions, we show the average effects, represented by diamonds instead of circles.
Figure 2: Recipient and household effects of cash transfers on wellbeing

4.2 Psychotherapy results
The studies that include effects on a household member found a significant effect of psychotherapy on the wellbeing of the direct recipient, average d = 0.662 (95%: 0.35, 0.97). This is close to the initial effect, as the average follow-up is two months after the therapy ended. We find a non-significant effect of psychotherapy on the wellbeing of the household member, average d = 0.352, (95% CI: -0.04, 0.74). We think this non-significance is likely due to the small sample size (i.e., the lack of power to detect an effect). Also, because of the small sample of studies (three in general, none of StrongMinds), we assume that the spillover ratio for psychotherapy, in general, is the same as StrongMinds, in particular. After taking the ratio of these two figures, we find that the household member receives ![]() = 0.352/0.662 = 53% (95% CI: 11%, 108%) of the recipient’s benefit. Recall that we used a simulation to find the confidence intervals.
= 0.352/0.662 = 53% (95% CI: 11%, 108%) of the recipient’s benefit. Recall that we used a simulation to find the confidence intervals.
Below, in Figure 3, we show a forest plot of the recipient and household effects of receiving psychotherapy. The plot has the same structure as the cash transfer forest plot, except recipients are indicated in blue.
Figure 3: Recipient and household effects of psychotherapy on wellbeing

4.3 Comparison of psychotherapy to cash transfers including household effects
The spillover effects for cash transfers and psychotherapy are summarised in Table 1 below.
Table 1: Household spillover effects for cash transfers and psychotherapy
| Intervention | Cash transfers | Psychotherapy |
|
Recipient effect (Cohen’s d) |
0.114*** |
0.662* |
| Household member effect (Cohen’s d) |
0.098** |
0.352+ |
| Spillover ratio (S) |
86% |
53% |
| Timepoints (follow-ups) | 10 | 5 |
| Interventions | 6 | 3 |
Note: 95% confidence intervals are placed in parentheses below point estimates
(*** p-value < 0.01, ** p-value < 0.01, * p-value < 0.05, + p-value < 0.01)
In the first two rows, we reiterate the spillover effects at the bottom of the forest plots. Below that, “Spillover ratio (S)” indicates the spillover ratio. The spillover ratio is the variable we use to estimate what share of the total effect a given household member receives due to the delivery of the interventions. At the bottom of the table, we note the number of outcomes (intervention-follow up combinations) and interventions used to make these calculations.
Note that the confidence interval for the cash transfers spillover ratio is wider (less certain) than the confidence interval for the psychotherapy spillover ratio. We might have expected the opposite pattern in uncertainty. This is because the inputs, the household and recipient effects, are more precisely estimated for cash transfers. The issue here is that the cash transfer estimates are closer in magnitude to zero. Since the spillover effect is a ratio, the simulation generates very large values when the denominator (the recipient effect) is close to zero. Hence, this potentially inflates uncertainty around the cash transfer spillover.
We summarise the key results from our analysis in Figure 4 below. In the top panel we review the average recipient and non-recipient household effects on psychotherapy and cash transfers. In the bottom panel, we show the estimated spillover ratios. Note that the estimated spillover ratios are in percent of recipient benefit experienced by each household member, not standard deviation changes in wellbeing.
Figure 4: Summary of household effects meta-analysis and the spillover ratio

We find that accounting for household spillovers reduces the cost-effectiveness advantage of psychotherapy relative to cash transfers; it is no longer 12 times more cost-effective. We find that psychotherapy is 8.8 times (95% CI: 1.7, 99.8) more cost-effective than monthly cash transfers. When comparing the charities that deploy these interventions, we estimate that StrongMinds is 9.5 times (95% CI: 1.3, 89.9) more cost-effective than GiveDirectly.
The slight differences between the psychotherapy versus monthly cash transfers comparison and the StrongMinds versus GiveDirectly comparison can be explained by the differences in the variables (effects and costs) that characterise them, as seen in Table 2 below. StrongMinds and GiveDirectly are good implementations of their larger interventions, so they will differ (be more cost-effective) from their interventions in general. StrongMinds is better than psychotherapy in general because it has a larger effect and a lower cost, and GiveDirectly is better than general cash transfers because it has a larger effect (but their costs are quite similar). This explains why StrongMinds has a higher cost-effectiveness advantage on GiveDirectly than psychotherapy has on monthly cash transfers.
In Table 2 we summarise the estimated household effects and their determinants. In the first column, we show the average household size we use. The spillover ratio is the same as presented in Table 1. The recipient effect is the same as the one used and explained in our previous reports (see cash transfers and psychotherapy). The household effect, as calculated using the previous three columns according to Equation 4 is given in the last column.
Table 2: Summary of estimated spillover effects and change in comparison
| Analysis | Non-recipient household size |
Spillover ratio |
Recipient benefit |
Household benefit |
Intervention cost |
| GiveDirectly |
3.93 |
86% |
1.05 |
4.61 |
$1,221 |
| StrongMinds |
4.85 |
53% |
1.69 |
6.06 |
$170 |
| Cash transfers |
3.80 |
86% |
0.40 |
1.71 |
$1,274 |
| Psychotherapy |
3.80 |
53% |
1.40 |
4.85 |
$360 |
Note: The 95% confidence intervals are in parentheses below the estimates. Using this table, you can use the household size, spillover share, recipient effect, and intervention cost to replicate our calculations.
In Table 3 we present the comparison of psychotherapy to cash transfers when using the entire household instead of just the recipient effect.
Table 3: Summary of change in comparison when household spillovers are added
| Recipient | Household | |||
| Comparison between StrongMinds and GiveDirectly |
11.59 |
9.46 |
||
| Comparison between psychotherapy and cash transfers |
12.40 |
8.76 |
||
Note: Both of these comparisons are in multiples of cost-effectiveness (the ratio of psychotherapy’s cost-effectiveness over cash transfers’ cost-effectiveness). The 95% confidence intervals are in parentheses below the estimates.
Readers might be surprised by the width of our confidence intervals (i.e., how uncertain our results are). Estimates relating only to the recipient are wider than in our previous reports, not because they are more uncertain, but because these are 95% CI instead of 90% CI (see footnote 12 where we explain why we misreported 90% CI as 95% CI in our previous reports and how we corrected this by using R instead of Guesstimate). Estimates relating to spillovers and the household analysis are wide because, in Monte Carlo simulations, confidence intervals typically increase when models increase in complexity.19 This is typically, but not always, the case as Table 3 illustrates. Our intuition suggests that household comparison should have more uncertainty than the individual comparison. This is not the case, as can be seen for the confidence intervals of the comparison between psychotherapy and cash transfers. We believe this is due to a property of ratios. With the household benefit, the cash transfer cost-effectiveness estimates (the denominators in the comparison ratios) are larger than in the individual analysis, thereby, they are less likely to generate values close to zero – and consequently generate very large values – in the Monte Carlo simulations of the comparison. Hence, the uncertainty in the individual comparison is wider when compared to the household comparison.
How might we assess that these are reasonable confidence intervals? Whilst we could compare them to those of other actors, unfortunately, we do not have this information. We would like to gauge them against GiveWell, but they do not quantify their uncertainty in their analyses. More importantly, we could test what our Monte Carlo simulations tell us about our estimates given the assumptions of our model.
Notably, interpreting our Monte Carlo simulations as probability distribution samples, our confidence intervals tell us that, given the assumptions of our models, there is less than a 2.5% chance that cash transfers are more cost-effective than psychotherapy. More detailed calculations on our Monte Carlo simulations show that, according to our models, there is a 1.46% chance that GiveDirectly is more cost-effective than StrongMinds (only 146 of our 10,000 simulations had GiveDirectly more cost-effective than StrongMinds), and a 0.63% chance that cash transfers are more cost-effective than psychotherapy. Furthermore, our model suggests there is a 56% chance that StrongMinds is eight or more times20 GiveWell states that they typically fund opportunities that are eight (or more) times more cost-effective than cash transfers. more cost-effective than GiveDirectly, and a 54% chance that psychotherapy is eight or more times cost-effective than cash transfers. Note that these percentages would differ in our robustness checks or if we made alternative modelling choices.
Finally, we display the updated results visually in Figure 5, which illustrates a simulation of the comparison between psychotherapy, StrongMinds, monthly cash transfers, and GiveDirectly. This time, the comparison includes the household effects. Each point is an estimate given by a single run of a Monte Carlo simulation. Lines with a steeper slope reflect higher cost-effectiveness in subjective wellbeing and mental health. Lines reflect the cost-effectiveness gradient of interventions. In this comparison, a $1,000 donation to StrongMinds is around 9 times (95% CI: 1, 90) more cost-effective than a comparable donation to GiveDirectly.
Figure 5: Comparison of cash transfers and household psychotherapy with household effects

Note: There is a cutoff at $1,000 for cash transfers because we considered it implausible for a cash transfer to cost less than $1,000 to send $1,000 (i.e., we truncated cost simulations, see footnote 18).
5. Robustness checks
In this analysis, we chose how to model certain variables and which data to use. We believe the default analysis we have presented is the best version of all these choices. For transparency, and for the reader’s information, we present alternative analyses that stem from different choices. Namely, we conduct robustness checks to assess how much our results change when we change the analysis. We recommend our default analysis, and recommend against, with varying strength, the alternative analyses. The alternative analyses are listed in the following section, presented in a rough order from those we weakly recommend against to those we strongly recommend against. We present the methods and results of each alternative analysis, as well as why we recommend against it, in more detail in Appendix C. We present how each alternative analysis would modify the cost-effectiveness advantage of psychotherapy relative to cash transfers in Table 4. The cost-effectiveness advantage of psychotherapy over cash transfers never drops below five times across all our robustness checks.
5.1 Alternative analyses
1. We model both charities with the same household size. In our default analysis, we modelled them with different household sizes because StrongMinds and GiveDirectly operate in different areas with different average household sizes. We weakly recommend against this analysis.
2. We keep Haushofer et al’s. (2019) breakdown of their results by whether the recipient of GiveDirectly cash transfers were men or women. In our default analysis, we aggregated these results because this was the only study in our analysis to split their analysis by gender, and because this split is not relevant to our analysis. Therefore, we moderately recommend against disaggregating the GiveDirectly data across gender.
3. We remove the second Swartz et al. (2008) follow-up because the benefit grows over time for the household member but declines for the recipient (which is unusual and might indicate an outlier). We moderately recommend against this, and keep the second Swartz et al. (2008) follow-up in our default analysis, because it seems presumptive to treat one effect size as an outlier when we have so few data points.
4. We only use psychotherapy data from low- and middle-income countries. In our default analysis, we consider that psychotherapy data from high-income countries can inform us about ![]() for interventions in low- and middle-income countries. We strongly recommend against this because it would mean relying solely on one study, Mutamba et al. (2018).
for interventions in low- and middle-income countries. We strongly recommend against this because it would mean relying solely on one study, Mutamba et al. (2018).
5. We use a frequentist method and model S solely with the data, not with the influence of a prior (i.e., we do not combine prior beliefs about spillovers with our current data). We have two alternative Bayesian analyses: one where we use all the priors provided by respondents in a survey (5a) and another where we only use priors provided by two GiveWell staff (5b). We explain this method further in Section 5.3 and Appendix C5. This is to illustrate how different prior beliefs could lead to different conclusions. Indeed, using the collective representation of a prior from every respondent in the survey improves the cost-effectiveness of psychotherapy, whereas, the collective representation of a prior from only the GiveWell respondents reduces the cost-effectiveness advantage of psychotherapy. In each case, we strongly recommend against these alternative analyses because we only collected a small sample of priors and we are unsure about how well our survey could capture people’s priors. One particular concern, raised after we ran the survey, is that the wording of the survey asked about people’s predictions about the effects on ‘wellbeing’ not ‘subjective wellbeing’, which might have biased responses.
6. Instead of using the Ratio of Averages to calculate the spillover ratios, other methods could be used, such as the Average of Ratios method (6a). However, in Appendix C6 we present reasoning and citations showing that Ratio of Averages is a better method. Instead of using a spillover ratio, we could use the average effect size on a household member (a raw benefit) multiplied by the non-recipient household size to determine the non-recipient household benefit (6b). However, this is also inappropriate because the raw benefit is not from the same data we use to determine the recipient effects of psychotherapy and cash transfers. Therefore, we very strongly recommend against both of these alternative analyses.
5.2 Alternative results
We present the results of running the alternative analyses in Table 4 below. Analyses that increase the cost-effectiveness advantage of psychotherapy compared to cash transfers relative to our default analysis are represented in green. Yellow represents the analyses which reduce the cost-effectiveness advantage of psychotherapy but not below eight times cash transfers.21 GiveWell states that they typically fund opportunities that are eight (or more) times more cost-effective than cash transfers. Red indicates analyses where the relative cost-effectiveness advantage of psychotherapy reduces to below eight times. In four analyses, the cost-effectiveness advantage of psychotherapy reduces to less than eight times. This illustrates that the greater than eight times cost-effectiveness advantage of psychotherapy relative to cash transfers is sensitive to modelling choices.
Table 4: Robustness checks
5.3 Adding priors
In our most involved robustness check we perform two Bayesian analyses, combining our data with priors obtained from a survey to produce a posterior estimate of the spillover ratio. The more informative (certain, smaller variance) the prior or the data are, the more weight they have relative to each other in determining the posterior. We have two versions of this robustness check: one using the priors from all ten survey respondents and one using only the priors from Alex Cohen and James Snowden (two GiveWell researchers who agreed to be named publically). Because of the small sample of respondents, the responses should not be taken to represent the views of GiveWell as an organisation nor effective altruism as a community. Whilst Bayes’ rule is a normative standard for updating beliefs, this is not a formal presentation of how a specific person’s prior should update in light of the data but an illustration for the reader. It is meant as an illustration because – as mentioned in Section 5.1.5 – there was a potential issue with the wording of our survey question and – as mentioned at the end of this section – the priors might be considered too certain.
For a summary of the results, see Table 5 below. The prior spillover ratio distributions were modelled as normal distributions, characterised by the average point estimate provided in the survey and the average standard deviation obtained using the confidence intervals provided in the survey. The spillover ratio distributions from the data are the same ones presented in our default analysis. The posterior spillover ratio distributions (a combination of the prior and data distributions) are obtained via grid approximation, a numerical method that can be used to estimate the posterior even when it is not analytically solvable (Johnson et al., 2021; McElreath, 2020). The final two columns show how using the posterior spillover ratios affects the cost-effectiveness advantage of psychotherapy relative to cash transfers (already presented in Table 4). For further details of the methods and results (including figures), please see Appendix C5.
Table 5: Summary results of the alternative Bayesian analyses
| Analysis | Intervention |
Prior Mean (SD) |
Data Estimate (95% CI) |
Posterior Mean (95% CI) |
StrongMinds versus GiveDirectly |
Psychotherapy versus cash transfers |
| Every respondent | Cash transfers |
69% |
86% (43%, 154%) |
74% (47%, 102%) |
9.56 (1.51, 81.18) |
8.92 (1.98, 93.34) |
| Psychotherapy |
43% |
53% (11%, 108%) |
46% (21%, 72%) |
|||
| GiveWell respondents | Cash transfers |
100% |
86% (43%, 154%) |
98% (79%, 117%) |
5.63 (0.95, 49.46) |
5.42 (1.23, 58.29) |
| Psychotherapy |
23% |
53% (11%, 108%) |
28% (10%, 45%) |
Note: The 95% confidence intervals are in parentheses below the estimates. For the prior, the standard deviation is in parentheses below the estimates.
Whilst this might provide the reader with a formal update to their understanding about spillovers for cash transfers and psychotherapy, we caution that this is potentially inappropriate. Our data is limited by a small number of studies and participants, but we believe readers should update further towards the data than this Bayesian analysis suggests. The priors presented by survey respondents seem too confident for one of the first subjective wellbeing analyses of household spillovers which means they are given too much weight in determining the posterior spillover ratio. To be clear, we (Joel and Samuel) think we also would have given too narrow priors if we had answered the survey before analysing the data. We think it is generally difficult to form and precisely describe an appropriate subjective prior, and our Bayesian analysis should be interpreted with that limitation in mind.
6. Limitations and future steps
The greatest limitation of this analysis is that it relies on a small number of data points (six studies for cash transfers, three studies for psychotherapy). This appears to be a gap in the evidence base for these interventions. If a household size is five people, then the household spillover benefit only needs to be 25% the size of the recipient’s to be as important as the recipient effect. Generally, if the spillover ratio > 1 / (household size – 1), where 1 is the direct recipient, then the non-recipient household effect is larger than the recipient effect. For example, if a recipient receives 1 unit of benefit, and the spillover ratio is 25%, then the non-recipient household benefit is also 1 unit (4 x 0.25). This condition seems plausible for many interventions, especially those aimed at benefiting the whole household (most poverty alleviation programmes, housing improvement interventions, air or water quality improvements, etc.). For that reason, we think household spillovers deserve more study and evidence collection.
Additionally, this was not a systematic search. However, we think it is sufficiently exhaustive because we searched studies collected in systematic searches (McGuire et al., 2020) and the MetaPsy database. Given the scarcity of evidence, if we had more time, we would try to make greater use of panel data that records changes in income and mental health. One complication with using the panel data is how to combine correlational data from the panels with the group differences from the intervention studies. We would also consult experts on whether employing more sophisticated Bayesian methods would make our estimates more accurate.
We currently assume the recipient effect and the household member effect are independent. However, this might not be true as these effects are likely correlated (dependent on each other). Dr Henrik Singmann recommended that we use a more sophisticated method which would allow us to incorporate the correlation between the recipient and household member effects when combining the effects from different studies (i.e., a joint meta-analysis).
We remain uncertain about several relationships that are important to the household spillover, such as the effect of household size on the spillover effect. At present, our underpowered models indicate small and non-significant relationships. A better way to test whether household size and composition affects household spillover is to make use of data where household sizes vary across recipients (not just across studies, as in our analysis). We could run this test using individual-level data (e.g., from Haushofer et al., 2019). However, this was outside the scope of our analysis.
A final limitation of our analysis is that we do not incorporate higher level uncertainty about our modelling and theoretical assumptions into our cost-effectiveness analysis. The uncertainty we convey in our confidence intervals is a product of uncertainty in the estimation of empirical parameters. We could introduce higher level uncertainty by representing how much we would weight each analysis decision (those in our robustness check and beyond). In the future – and with more time – we will improve our modelling to better capture our theoretical uncertainty.
7. Conclusion
We update our earlier subjective-wellbeing-based cost-effectiveness comparison of psychotherapy and cash transfers by including an estimate of the total household effects. Our previous analysis only investigated the effects on recipients. After including the household spillover effects, psychotherapy is 9 times (95% CI: 2, 100) more cost-effective than cash transfers and StrongMinds is 9 times (95% CI: 1, 90) more cost-effective than GiveDirectly. These are only small reductions from our previous 12 times estimates. Our household analysis consists of a relatively small number of studies (eight for cash transfers, three for psychotherapy). We conducted several robustness checks. We found psychotherapy to be at least five times more cost-effective than cash transfers in all cases.
We found eight cash transfer and three psychotherapy studies of household spillover effects. There were 45 studies of cash transfers in our meta-analysis and hundreds of psychotherapy studies in the wider literature that recorded direct recipient effects. Given that discrepancy in the quantity of evidence, it seems there is a gap in the literature surrounding household effects that should be addressed by further research. But this gap is potentially easy to close if investigators have the resources to survey an additional household member with a brief subjective wellbeing or mental health questionnaire.
We would like to thank the following people for their help: Victoria Baranov, Pim Cuijpers, Ismail Guennouni, Caspar Kaiser, Crick Lund, Vikram Patel, Clara Miguel Sanz, Henrik Singmann, and James Snowden. We would also like to thank every participant in our household spillover prior survey and every participant in our seminar on household spillovers.
Appendix A: Description of spillover studies
A1. Cash transfer studies
Angeles et al. (2019) studied a pair of caregivers (n = 631) and children (n = 1,366) in the Malawi Social Cash Transfer (SCTP). They found that the spillover effect was 38% as large as the recipient effect after the cash transfer at the two-year follow-up.
In the Kenya Cash Transfer for Orphans and Vulnerable Children (CT-OVC), Handa et al. (2014) analysed the cash transfer’s effects on the adults in the household who received the transfer (n = 1,805). Kilburn et al. (2016) studied the cash transfer’s effects on the adolescent sample (the spillovers, n = 2,006). However, these studies use different follow-ups across adult and adolescent studies. Handa et al. (2014) followed up two years after the cash transfer began, and Kilburn et al. (2016) followed up four years after the cash transfer began. Ideally, we would compare effects on adults and children at the same follow-up. They found that the spillover effect was as large as the effect on the recipient.
In Ohrnberger et al. (2020), which studied the South African Child Support Grant, the average benefit for mental health for other household members (n = 6,808) was 63% that of the recipient (n = 10,925). The characteristics of the non-recipient household members were not specified. Since surveys of adults are more common, we assume it was another adult respondent. The study has an unusually large sample size since the data came from the South Africa Income Dynamics panel survey. The large sample size and free to access data makes it a candidate for an individual level re-analysis.
Baird et al. (2013) found that the spillover effect on the siblings (n = 1,421) of a young woman who received unconditional cash transfers (UCT) was 13% as beneficial as it was for the recipient (n = 1,820). This figure was 33% for the conditional cash transfer (CCT ) arm of the trial (n = 1,421). These figures are relatively low because the second time points reported negative (but non-significant) spillover effects on the sibling.
The spillover effects from the Mexican Oportunidades conditional cash transfer come from Ozer et al. (2009; 2011). In Ozer et al. (2009, 2011), the benefits to the child’s anxiety ( n = 6,242) are 1.75 times the benefit to the mother’s depression (n = 945). This is the only household spillover study to come from Latin America.
In Haushofer et al. (2019), which studied a GiveDirectly cash transfer, the benefit the recipient’s partner (n = 881) receives is 1.48 times the benefit received by the recipient (n = 1,010). But this changes depending on whether the woman or man receives the transfer. Haushofer et al. (2019) disaggregate the spillover effect depending on the gender of the recipient and found that it is better if the woman receives the cash transfer. They disaggregate the effect based on gender because the paper was primarily investigating cash transfer’s effect on intimate partner violence.
A2. Psychotherapy studies
Mutamba et al. (2018) measured the effect of 12 sessions of group interpersonal psychotherapy delivered by lay community health workers to caregivers (both male and female, but majoritarily female) of children with nodding syndrome in Uganda (a low-income country). Nodding syndrome is characterised by seizures with no known cause or cure, most common in Sub-Saharan Africa (CDC, 2012). A limitation of the study is that households with nodding syndrome may respond differently to psychotherapy than the broader population. In the study, 73 participants from seven villages received usual care and group interpersonal psychotherapy, and 69 from six other villages received usual care (the control group). An important limitation of this study is that participants were non-randomly assigned to the intervention or control group (but see footnote 6). Effect sizes were obtained one and six months after the end of the intervention. Depression levels were measured with the MINI Neuropsychiatric Interview for the caregivers and the Depression Self-rating Scale for the children with nodding syndrome.
Kemp et al. (2009) conducted an RCT of a six-week EMDR treatment for persistent PTSD symptoms due to a motor vehicle accident in children between 6 and 12 years old. There were 12 child-parent pairs in the treatment group and 14 child-parent pairs in the wait-list control group. After treatment, the depression levels of the children were measured with a self-report measure of the Child Depression Scale, and the parents’ (who did not receive therapy) mental health was measured with the 12-items General Health Questionnaire (GHQ-12). There was a significant difference in GHQ-12 levels between control and treatment group parents, so we used the difference of differences between baseline and post-treatment to adjust for this. This intervention was conducted in Australia.
Swartz et al. (2008) conducted an RCT of nine sessions of modified interpersonal therapy for depressed mothers of children with psychiatric illness. The fact that both the mothers and children having mental illnesses could weaken the generalizability of the findings. One way this could play out is if children with mental illness are more or less sensitive to changes in their mother’s depression than children in the broader population. There were 26 mother-child pairs in the treatment group and 21 mother-child pairs in the ‘treatment as usual’ control group. Effect sizes were obtained after the end of the intervention (which lasted three months) and six months after the end of the intervention. Depression levels for the mothers were obtained with the Beck Depression Inventory and depression levels for the children were obtained with the child self-report Children’s Depressive Inventory. This intervention was conducted in the United States.
Appendix B: Estimating the household size
For the household sizes in the StrongMinds versus GiveDirectly comparison, we use the average household size for the African countries in which these charities operate. StrongMinds mostly operates in Uganda, which has a relatively large household size (5.9). GiveDirectly appears to operate mostly in Kenya, which has a smaller household size (4.7). We use country-level information because we did not collect the more relevant household information from the psychotherapy studies included in our previous meta-analysis.
We calculate average household sizes by averaging the latest available data from the United Nations Population Division (2019a), with average rural household sizes in these countries. Rural household size data comes from the Global Data Lab. We do this because StrongMinds and GiveDirectly operate mainly in rural or suburban areas. When available, we combine this information with the average household sizes reported in published studies (Banerjee et al., 2020; Egger et al., 2020; Haushofer et al., 2020a, 2020b; Haushofer & Shapiro, 2016, 2018; Kimani et al., 2020; McIntosh & Zeitlin, 2020). We then weight the average household sizes and the standard deviations,22 The United Nations Population Division (2019a) also provides percentages of households with 1, 2-3, 4-5, 6+ members for each country. We sample 100 values for each country, based on these percentiles, to obtain standard deviations values for each country. For the 2-3 category, we treat 2 members as 40% and 3 members as 60% of this category. For the 4-5 category, we treat 4 members as 60% and 5 members as 40% of this category. For the 6+ category, we treat 6 members as 40%, 7 members as 30%, 8 as 20%, and 9 as 10% of this category. based on each charity’s share of activity (according to how many people StrongMinds treats or how many grants GiveDirectly allocates) in these countries.
We assume that, in general, psychotherapy and cash transfer interventions could be deployed in any area of Sub-Saharan Africa. Hence, for the overall intervention-level comparison, we assign the same household size to psychotherapy and cash transfers. We use household size information for Sub-Saharan Africa (M = 4.8, SD = 0.9.23 We estimated the standard deviation based on the quantiles provided by the United Nations Population Division (2019b)) from the United Nations Population Division (2019b).
In each case, we obtain the non-recipient household size (the household size not counting the direct recipient of the intervention) by subtracting 1 from the average household size. When we simulate household sizes we centre the distributions24 We use truncated normal distributions (using the msm package; Jackson, 2011) for our Monte Carlo simulations of non-recipient household size to avoid the non-recipient household size being below zero. on their averages and stipulate their standard deviations using the estimated standard deviations of the household size.
For StrongMinds, we find a non-recipient household size of 4.85 (95% CI: 1.01, 8.94). For GiveDirectly, the non-recipient household size is 3.93 (95% CI: 0.5, 8.27). We use the same non-recipient household size of 3.80 (95% CI: 2.03, 5.56) for psychotherapy and cash transfers.
Table B1: Household size and share of charity activity in each country
| Country |
Average Household Size |
StrongMinds |
GiveDirectly |
| DRC | 5.3 | 0.00% | 2.00% |
| Kenya | 4.7 | 0.00% | 61.11% |
| Liberia | 5.8 | 0.00% | 3.73% |
| Malawi | 5.0 | 0.00% | 7.01% |
| Rwanda | 4.8 | 0.00% | 7.00% |
| Togo | 4.9 | 0.00% | 4.13% |
| Uganda | 5.9 | 79.56% | 15.03% |
| Zambia | 5.9 | 20.44% | 0.00% |
Appendix C: Robustness checks
C1. Effects if we assume equal household sizes
In our main analysis, we estimate the household size based on the household sizes we expect StrongMinds and GiveDirectly beneficiaries to have. We could generalise our comparison of StrongMinds and GiveDirectly as if they were being deployed to a larger (and the same) area of activity by assigning them the same household size when calculating the household benefit of each intervention. We obtain a household size (and its standard deviation) in the same way as for the main analysis. Except here we weight these values according to the countries’ respective population sizes (from the latest 2020 data by the World Bank). We obtain a weighted average household size, not counting the direct recipient, of 4.25 (95% CI: 0.63, 8.58).
There are two ways household size can influence the comparison between interventions. First, if recipients of one intervention have larger households, then the household effect will be relatively larger. Second, since spillover effects are larger for cash transfers, larger household sizes (even if equal between interventions) will make cash transfers appear favourable.
Using the same household size reduces the cost-effectiveness advantage of StrongMinds relative to GiveDirectly down to 8 (95% CI: 1, 58) times more cost-effective.
C2. Disaggregating GiveDirectly’s effect across gender
The results of the GiveDirectly intervention (see Haushofer et al., 2019) are split across gender, which is the only instance of such a split in our data. When we disaggregate the GiveDirectly effect into two effects split across gender, it increases ![]() to 96% (95%: 41%, 329%) and decreases the relative cost-effectiveness advantage of psychotherapy over cash transfers. Psychotherapy would then be 8 times (95%: 1, 90) more cost-effective than cash transfers, and StrongMinds would be 9 times (95%: 1, 82) more cost-effective than GiveDirectly. We do not think this appropriate because this split is not relevant to our analysis and is the only instance of such a split in our data.
to 96% (95%: 41%, 329%) and decreases the relative cost-effectiveness advantage of psychotherapy over cash transfers. Psychotherapy would then be 8 times (95%: 1, 90) more cost-effective than cash transfers, and StrongMinds would be 9 times (95%: 1, 82) more cost-effective than GiveDirectly. We do not think this appropriate because this split is not relevant to our analysis and is the only instance of such a split in our data.
C3. Removing Swartz et al.’s (2008) second follow-up
The follow-up from Swartz et al. (2008) appears ‘odd’ because it suggests that the household member effect grows while the recipient effect declines over time. Removing the follow-up from Swartz et al. (2008) affects the analysis by lowering ![]() to 36% (95%: 1%, 81%) and reducing the relative cost-effectiveness advantage of psychotherapy over cash transfers. Psychotherapy would then be 7 times (95%: 1, 79) more cost-effective than cash transfers, and StrongMinds would be 7 times (95%: 1, 68) more cost-effective than GiveDirectly. Nevertheless, we think it seems presumptive to treat one effect size as an outlier when we have so little data.
to 36% (95%: 1%, 81%) and reducing the relative cost-effectiveness advantage of psychotherapy over cash transfers. Psychotherapy would then be 7 times (95%: 1, 79) more cost-effective than cash transfers, and StrongMinds would be 7 times (95%: 1, 68) more cost-effective than GiveDirectly. Nevertheless, we think it seems presumptive to treat one effect size as an outlier when we have so little data.
C4. Using data from low- and middle-income countries
If we use only data from low- and middle-income countries (like our previous reports) we are left with only two effect sizes from one study in Uganda (Mutamba et al., 2018) when calculating the psychotherapy spillover ratio. Unfortunately, this study did not randomly allocate participants to the treatment and control conditions (but see footnote 6). Furthermore, we should be wary of analysis with only one study.
When using only Mutamba et al. (2018), findings become more uncertain. The psychotherapy spillover ratio ![]() decreases to 38% (95% CI: -2%, 92%). The analysis for cash transfers remains unchanged as all effect sizes are already from low- and middle-income countries. Therefore, we find that psychotherapy is 7 (95% CI: 1, 84) times more cost-effective than monthly cash transfers. When comparing the charities that deploy these interventions, we estimate that StrongMinds is 7 (95% CI: 1, 73) times more cost-effective than GiveDirectly.
decreases to 38% (95% CI: -2%, 92%). The analysis for cash transfers remains unchanged as all effect sizes are already from low- and middle-income countries. Therefore, we find that psychotherapy is 7 (95% CI: 1, 84) times more cost-effective than monthly cash transfers. When comparing the charities that deploy these interventions, we estimate that StrongMinds is 7 (95% CI: 1, 73) times more cost-effective than GiveDirectly.
C5. Adding priors
C5.1 Summary
An important piece of feedback on our previous analysis stemmed from stakeholders expressing a belief that the spillover ratio for psychotherapy would be much smaller than the spillover for cash transfers. This motivated us to compare and contrast prior beliefs about spillovers with the data we obtained.
We asked people interested in our research to provide their prior beliefs about the spillover ratios for cash transfers and psychotherapy in a survey. Respondents were asked to provide a point estimate and 95% confidence intervals for both the cash transfers spillover ratio and the psychotherapy spillover ratio. The survey was advertised on the Effective Altruism Forum, Twitter, and effective altruism-related Slack channels. It asked the following questions:
1. How much do you expect a household member’s wellbeing to benefit from another household member receiving the following intervention (relative to the direct recipient’s benefit)?
Answers were given with a matrix of options between “Less than 0% (negative effects)” to “Greater than 100%” with steps of 10% in between.
2. What’s the range of reasonable values you think the (cash transfer/psychotherapy) spillover will take? Loosely speaking, what’s your 95% confidence interval?
Answers were given in an open text input, which we converted into upper and lower values.
In future surveys, we will ask specifically about “subjective wellbeing” instead of “wellbeing”, which can be potentially misleading if the respondent does not think subjective wellbeing is an accurate measure of wellbeing.
We posited that respondents might have some insights into cash transfers and psychotherapy and their guesses may provide additional information about household spillovers. By combining these guesses, we can build a prior that benefits from the “wisdom of crowds”. Note that we are not directly expressing the priors of the respondents themselves, but building a collective representation of a prior – as an illustration – with the methods presented below. Therefore, we do not intend this as a formal presentation of how a specific person’s prior should update in light of the data but as an illustration for the reader.
Ten participants25Originally 11, but we took out one response from an HLI staff member, because we considered that their prior was already influenced by the data. responded to our survey. Two were GiveWell staff members (Alex Cohen and James Snowden – who agreed to be mentioned by name). The rest were individuals involved in effective altruism. We form two collective prior representations: one for everyone who responded to the survey (including the GiveWell staff members) and one using only the answers from the GiveWell staff members. As this is a very small number of respondents, it cannot serve as a global representation of GiveWell as an organisation nor effective altruism as a community. We represent these using normal distributions26 It has been suggested to us that we might use Cauchy distributions instead. Cauchy distributions are popular for priors and there was a possibility that they might make for weaker priors (i.e., they would let the data influence the posterior more) than our current normally distributed priors. However, our brief investigation of this alternative prior specification found that the posteriors were even more influenced by the priors (i.e., the issues were exacerbated); hence, we decided to keep using normal priors. based on the answers provided in our survey. The mean of the distribution is the average of the point estimates. For each respondent, we obtain a standard deviation based on their confidence intervals27 Using SD = (upper – lower)/3.92 and average these to have a standard deviation for the distribution.
Below, we present Table 5 again (now called Table C1) to summarise the results of our Bayesian analysis.
Table C1: Summary results of the alternative Bayesian analyses
| Analysis | Intervention |
Prior |
Data |
Posterior |
StrongMinds versus GiveDirectly |
Psychotherapy versus cash transfers |
| Every respondent | Cash transfers |
69% |
86% (43%, 154%) |
74% (47%, 102%) |
9.56 (1.51, 81.18) |
8.92 (1.98, 93.34) |
| Psychotherapy |
43% |
53% (11%, 108%) |
46% (21%, 72%) |
|||
| GiveWell respondents | Cash transfers |
100% |
86% (43%, 154%) |
98% (79%, 117%) |
5.63 (0.95, 49.46) |
5.42 (1.23, 58.29) |
| Psychotherapy |
23% |
53% (11%, 108%) |
28% (10%, 45%) |
Note: The 95% confidence intervals are in parentheses below the estimates. For the prior, the standard deviation is in parentheses below the estimates.
The average prior for all respondents predicts the cash transfer spillover ratios, ![]() (M = 69%, SD = 17%), to be higher than the psychotherapy spillover ratio,
(M = 69%, SD = 17%), to be higher than the psychotherapy spillover ratio, ![]() (M = 42.5%, SD = 16%). These results predict lower spillover ratios for both cash transfers and psychotherapy than the data suggests (
(M = 42.5%, SD = 16%). These results predict lower spillover ratios for both cash transfers and psychotherapy than the data suggests (![]() = 86%,
= 86%, ![]() = 53%). This prediction underestimated the size of the spillover effects, but predicted similar – albeit slightly smaller – differences between the interventions than we found (a difference of 27% rather than 33%). The representation of the prior based on responses from GiveWell staff members28 Only one GiveWell respondent provided a confidence interval, so this is the one we used to determine the standard deviation of the distribution. predicts the cash transfer spillover ratio,
= 53%). This prediction underestimated the size of the spillover effects, but predicted similar – albeit slightly smaller – differences between the interventions than we found (a difference of 27% rather than 33%). The representation of the prior based on responses from GiveWell staff members28 Only one GiveWell respondent provided a confidence interval, so this is the one we used to determine the standard deviation of the distribution. predicts the cash transfer spillover ratio, ![]() (M = 100%, SD = 10%) to be higher than the psychotherapy spillover ratio,
(M = 100%, SD = 10%) to be higher than the psychotherapy spillover ratio, ![]() (M = 22.5%, SD = 10%), representing a belief that the psychotherapy spillover is much lower than the cash transfer one.
(M = 22.5%, SD = 10%), representing a belief that the psychotherapy spillover is much lower than the cash transfer one.
We use a Bayesian analysis to combine the priors and the data to produce a posterior estimate of the spillover ratio. The more informative (certain, smaller variance) the prior or the data are, the more weight they will have relative to each other in determining the posterior.
When we combine the whole survey’s representation of collective prior with our data, we get a posterior psychotherapy spillover ratio of 46% and posterior cash transfer spillover ratio of 74%. Therefore, the advantage of psychotherapy compared to cash transfers increased relative to our default analysis: psychotherapy stays 9 times more cost-effective than cash transfers, and StrongMinds increases to 10 times more cost-effective than GiveDirectly. This is because the spillover ratio of cash transfers was predicted to be closer to that of psychotherapy than we found in the data.
When we combine the GiveWell staff’s representation of a prior with our data, we get a posterior psychotherapy spillover ratio of 28% and posterior cash transfer spillover ratio of 98%. Therefore, the relative advantage of psychotherapy compared to cash transfers decreases compared to our default analysis: psychotherapy becomes 5 times more cost-effective than cash transfers, and StrongMinds becomes 6 times more cost-effective than GiveDirectly. This is because the spillover ratio of cash transfers was predicted to be much further from that of psychotherapy than we found in the data.
As explained in Section 5, this analysis might provide the reader with a formal update to their understanding about spillovers for cash transfers and psychotherapy, but we must caution that this is potentially inappropriate. Whilst our data is limited by a small number of studies and participants, we believe people should update further towards the data than this analysis suggests. If we (Samuel and Joel) were to specify a prior, it would be more uncertain than those formed from the survey responses. We recommend against these alternative analyses because of the small sample of priors, our uncertainty about how well our survey could capture people’s priors, and our concern that using “wellbeing” instead of “subjective wellbeing” in the wording of the question might have biased responses. Finally, we would like to reiterate that this was a robustness check and an illustrative exercise, not a formal evaluation of anyone’s priors.
Specifying the right priors is an important difficulty when engaging in Bayesian analyses. Perhaps we can find an ‘in-between’ prior that represents both people’s prior beliefs about the relative distance between the cash transfers and psychotherapy spillovers, whilst being uncertain enough to be open to the data (see Section C5.5).
C5.2 Method
In a Bayesian approach, the spillover ratios ![]() and
and ![]() are considered ‘continuous random variables’. That means they can take on a range of possible outcomes on a continuum between -∞ and +∞, described by a probability distribution. Each distribution is specified according to a probability density function (pdf) that defines the relative probability of the ratios falling within a particular range of outcomes. For example, a spillover ratio may be more likely to fall between 0% and 100% than between -50% and 50%. We must define the prior distributions for the spillover ratios and the distributions provided by the data then combine the two to obtain the posterior distributions.
are considered ‘continuous random variables’. That means they can take on a range of possible outcomes on a continuum between -∞ and +∞, described by a probability distribution. Each distribution is specified according to a probability density function (pdf) that defines the relative probability of the ratios falling within a particular range of outcomes. For example, a spillover ratio may be more likely to fall between 0% and 100% than between -50% and 50%. We must define the prior distributions for the spillover ratios and the distributions provided by the data then combine the two to obtain the posterior distributions.
The posterior will be shaped by both the prior and the data relative to their position (higher or lower in the space between -∞ and +∞) and how informative they are. The narrower (the less variance, the more informative) the prior and data distribution are (relative to each other), the more they will influence the posterior; in other words, if you are confident in your original belief, new evidence will barely update you, but if you have have weak priors, the evidence will change your mind a lot.
Our data distributions are positively skewed because they are ratios with denominators that can be close to zero and create large values, see Section 4.3. Skewed distributions make it difficult to analytically derive the posterior from our prior and data distributions. However, a typical process is to approximate the posterior using the grid approximation technique, which can easily be implemented in R (Johnson et al., 2021; McElreath, 2020). We divide a space of possible spillover ratio outcomes between -100% and +300% into 10,000 discrete outcomes (-100%, -99.96%, -99.92%, …, 299.96%, 300%). The more discrete parts, the more precise our approximation. Each part is like a snippet of the full image of the posterior. The more snippets the more precisely you can see the posterior, a bit like resolution (see Johnson et al.’s rainbow image illustration). In other words, we are approximating something continuous, the posterior pdf, by breaking it down into many discrete parts.
Once we have the grid, we represent the probability density across these discrete values according to the prior’s pdf and according to the data’s pdf, respectively (i.e., for discrete outcome X what is the probability density according to the prior and according to the data). According to Bayes’ rule, we approximate the posterior pdf by multiplying the representations of the prior’s pdf and data’s pdf across each value of the grid, which we then normalise (divide by the sum of every prior-data multiplication across the grid). We can then randomly sample 10,000 values of the spillover ratio from this normalised, approximated posterior pdf to describe the posterior and use it in the next steps of our analysis.
For the priors, we obtain the means and standard deviations based on the estimates provided by respondents to our survey. We then assume that the prior distributions of the spillover ratios are normally distributed and build the prior pdfs accordingly.29 Using the dnorm function in R. We use the ratio of the Monte Carlo simulated recipient effect distribution and Monte Carlo simulated household member effect distribution to obtain the data pdfs.30 Using the density function in R. We then use the sampled posterior distribution as our spillover distribution and the mean of this distribution for the next steps of the analysis (i.e., calculating the household benefit and the cost-effectiveness).
C5.3 Results: All respondents
In this analysis, we use the data from every survey response. For ![]() , combining the data (53%) with the prior (42.5%) results in a posterior of 46% (95% CI: 21%, 72%). In Figure C1, the prior distribution is in pink, the data distribution is in blue, and the posterior distribution is in purple. The circles represent the mean of the prior and posterior distributions as well as the point estimate for the spillover ratio from the data. Observing the graph, one can tell that the prior distribution is narrower than the distribution defined by the data; hence, the posterior average is closer to the prior than the data.
, combining the data (53%) with the prior (42.5%) results in a posterior of 46% (95% CI: 21%, 72%). In Figure C1, the prior distribution is in pink, the data distribution is in blue, and the posterior distribution is in purple. The circles represent the mean of the prior and posterior distributions as well as the point estimate for the spillover ratio from the data. Observing the graph, one can tell that the prior distribution is narrower than the distribution defined by the data; hence, the posterior average is closer to the prior than the data.
Figure C1: Grid approximation of the psychotherapy spillover ratio posterior

For ![]() , combining the data (86%) with the prior (69%) results in a posterior of 74% (95% CI: 47%, 102%), shown in Figure C2 below.
, combining the data (86%) with the prior (69%) results in a posterior of 74% (95% CI: 47%, 102%), shown in Figure C2 below.
Figure C2: Grid approximation of the cash transfer spillover ratio posterior

When we use these posterior spillover ratios in the rest of the analysis, we find that psychotherapy is 9 (95% CI: 2, 93) times more cost-effective than monthly cash transfers. When comparing the charities that deploy these interventions, we estimate that StrongMinds is 10 (95% CI: 2, 81) times more cost-effective than GiveDirectly. So when we incorporate priors, our results do not change much, although, psychotherapy’s cost-effectiveness advantage slightly improves because the average prediction is that there is a smaller difference between the spillover ratios than the data suggests.
C5.4 Results: Only GiveWell respondents
In this version of the analysis, we only use the priors provided by the two GiveWell staff members. For ![]() , combining the data (53%) with the prior (22.5%) results in a posterior of 28% (95% CI: 10%, 45%), see Figure C3 below. The prior distribution is in red, the data distribution is in blue, and the posterior distribution is in purple. The circles represent the mean of the prior and posterior distributions as well as the point estimate for the spillover ratio from the data.
, combining the data (53%) with the prior (22.5%) results in a posterior of 28% (95% CI: 10%, 45%), see Figure C3 below. The prior distribution is in red, the data distribution is in blue, and the posterior distribution is in purple. The circles represent the mean of the prior and posterior distributions as well as the point estimate for the spillover ratio from the data.
Figure C3: Grid approximation of the psychotherapy spillover ratio posterior

For ![]() , combining the data (86%) with the prior (100%) results in a posterior of 98% (95% CI: 79%, 117%), see Figure C4 below.
, combining the data (86%) with the prior (100%) results in a posterior of 98% (95% CI: 79%, 117%), see Figure C4 below.
Figure C4: Grid approximation of the cash transfer spillover ratio posterior

With these posterior spillover ratios, we find that psychotherapy is 5 (95% CI: 1, 58) times more cost-effective than monthly cash transfers. When comparing the charities that deploy these interventions, we estimate that StrongMinds is 6 (95% CI: 1, 49) times more cost-effective than GiveDirectly.
C5.5 Specifying a weaker prior
One concern that is applicable to any Bayesian analysis is whether the choice of a prior is appropriate. As mentioned in Section 5.3, the priors we (Joel and Samuel) would have specified in the past would likely have been as narrow as the priors built from the responses to our survey. However, after seeing how narrow priors can be resistant to the data and comparing them to the weakly informative priors that researchers use in new areas of inquiry, we would now specify weakly informative priors in our future Bayesian analyses.
What may a weakly informative prior have looked like for spillover ratios? We present some tentative thoughts about this question. We do this to illustrate how weaker priors will allow for more influence from the data on the posterior. We also do this to provide some thoughts about how a prior could be formed for spillover ratios. This is only exploratory and illustrative, it does not represent a particular prior from us.
If we define a normally distributed prior for spillover ratios we need to pick a mean and standard deviation. As mentioned earlier, we think the standard deviation should be large to reflect our uncertainty. Furthermore, with a normally distributed prior, values outside of three times the standard deviation are considered to have negligible probabilities and we do not want to exclude some plausible spillover ratios by setting a standard deviation that is too small. A more difficult question is where to set the mean. Perhaps, a generally weakly informative prior is one with a mean of 50% and a standard deviation of 25%, so that 95% of the probability is contained between 0% and 100%, with less than 2.5% probability that the spillover ratio would be above 100% and less than 2.5% probability that it would be below 0%. It seems reasonable that a spillover ratio might be between 0 and 100%, but less likely (although not impossible) that it would cause negative effects or provide a greater effect to the household than to the direct recipients.
Additionally, in defining a weakly informative prior, we could use information we presented about the spillover mechanisms (see Section 1.2). However, it is unclear exactly how to do so (notably because data presented in terms of correlation coefficients is constrained between -1 and 1) and this would take time beyond the scope of this illustration. Briefly, we could consider that the evidence that GiveDirectly recipients use a large amount of the cash transfers for common goods suggests we might set the mean of our prior higher than 50%.
If, in the case of cash transfers, we are shifting our mean closer to 100%, we might want to tweak the distribution (potentially with skew) so that shifting the mean up does not suggest that spillover ratios above 100% are much more likely (but still a bit more likely). While not impossible, it might not be highly probable as this would mean recipients are contributing something to the household that is much more valuable to household members than to themselves. Conversely, if one would argue for shifting the mean for psychotherapy below 50% – this is an example, we are not taking a stance here – we would also want to tweak the distribution so that shifting the mean down does not suggest that it is more likely that the intervention has negative effects on the household members. Namely, one can believe a spillover ratio might be low, without believing it is likely to be negative. This sort of modification is beyond the scope of this illustration.
Let us briefly illustrate for the reader what a more uncertain, ‘in-between’ prior might look like, based on the reasoning in the previous paragraph. Let us set the prior for the psychotherapy spillover ratio as ‘low’ with a mean of 30% and a standard deviation of 25%. And let us set the cash transfers spillover ratio as ‘high’ with a mean of 80% and a standard deviation of 25%. This results in a posterior cash transfers spillover of 82% (95% CI: 49%, 119%) and a posterior psychotherapy spillover ratio of 43% (95% CI: 11%, 76%). Hence, it results in posteriors that are more ‘in-between’ the prior and the data. When we use these posteriors in our analysis, it makes psychotherapy 8 times (95% CI: 2, 83) more cost-effective than cash transfers and StrongMinds 8 times (95% CI: 1, 73) more cost-effective than GiveDirectly. See Figures C5 and C6 for the graphical representations. Figure C6 clearly illustrates how a more uncertain prior makes for a posterior that is more ‘in-between’ the prior and data.
Figure C5: Grid approximation of the cash transfers spillover ratio posterior

Figure C6: Grid approximation of the psychotherapy spillover ratio posterior

C6. Alternative methods for calculating spillovers
There are methods for aggregating the spillover ratio S other than the Ratio of Averages (RoA) which we discussed in Section 3.1. We present two alternatives below, even though we think both are inferior methods to the RoA.
With the Average of Ratios (AoR) we get a ratio for every pair of effect sizes and then obtain an average of ratios with our aforementioned meta-analysis method:

Whilst using ratios, in general, can be problematic and produce biased estimates (Jasieński & Bazzaz, 1999), it has been reported, based on simulations and principles, that RoA is less biased and more appropriate than AoR (Hamdan et al., 2006; Stinnett & Paltiel, 1996). Furthermore, because we are using effect sizes in Cohen’s d, the denominator in the ratio (the recipient effect) can get close to 0 and produce unreasonably ‘wild’ ratios for individual pairs of the recipient and household effect sizes. RoA does not seem to be nearly as sensitive to outliers.
If we calculate S using the AoR, we find that ![]() = 82% (95% CI: 36%, 127%) and
= 82% (95% CI: 36%, 127%) and ![]() = 39% (95% CI: 14%, 64%). Therefore, we find that psychotherapy is 7 (95% CI: 2, 81) times more cost-effective than monthly cash transfers. When comparing the charities that deploy these interventions, we estimate that StrongMinds is 8 (95% CI: 1, 68) times more cost-effective than GiveDirectly.
= 39% (95% CI: 14%, 64%). Therefore, we find that psychotherapy is 7 (95% CI: 2, 81) times more cost-effective than monthly cash transfers. When comparing the charities that deploy these interventions, we estimate that StrongMinds is 8 (95% CI: 1, 68) times more cost-effective than GiveDirectly.
Another method could be to simply attribute the average non-recipient benefit to every household member other than the direct recipient of the intervention. Thereby, the household benefit would be obtained with (where “HH” means household.):
![]()
This is instead of:
![]()
So, for cash transfers we add 3.80*0.09 = 0.34 to the total benefit, and for psychotherapy we add 3.80*0.35 = 1.33 to the total benefit. Here, we find that psychotherapy is 13 (95% CI: 4, 91) times more cost-effective than monthly cash transfers. For GiveDirectly we add 3.93*0.09 = 0.35 to the total benefit, and for StrongMinds we add 4.85*0.35 = 1.70 to the total benefit. When comparing the charities that deploy these interventions, we estimate that StrongMinds is 17 (95% CI: 5, 66) times more cost-effective than GiveDirectly.
Using this raw benefit seems inappropriate because it is not from the same data we use to determine the recipient effects of psychotherapy and cash transfers. Unfortunately, that data does not contain sufficient household information. So we use other data to determine a spillover ratio S that we can then input into our model. As we explained previously, we think that looking at the relative benefits (the ratio) will be more appropriate than the absolute effects. We think this because it seems most plausible that the recipient and the household spillover effects are related and a ratio accounts for that.

